アルゴリズム

[Python] ネヴィル補間の実装方法

2025-04-15更新日: 2025-04-15

ネヴィル補間は、与えられたデータ点に対して多項式補間を行う手法です。

Pythonでの実装は、再帰的な関数を用いて行います。

ネヴィルの補間公式は次のように定義されます：

$P_{i, j} (x) = \frac{(x - x_{j}) P_{i, j - 1} (x) - (x - x_{i}) P_{i + 1, j} (x)}{x_{i} - x_{j}}$

ここで、 $P_{i, i} (x)$ はデータ点 $(x_{i}, y_{i})$ を通る補間多項式です。

Pythonでは、リストやNumPy配列を使ってデータ点を管理し、再帰的に補間を計算します。

目次から探す

ネヴィル補間とは
ネヴィル補間の数式とアルゴリズム
Pythonでのネヴィル補間の実装
実装例：Pythonコードの解説
ネヴィル補間の応用例
ネヴィル補間の計算効率と最適化
まとめ

ネヴィル補間とは

ネヴィル補間は、与えられたデータ点を用いて新しい点の値を推定するための数値解析手法の一つです。

この手法は、特に多項式補間において有効であり、再帰的な計算を用いて補間多項式を構築します。

ネヴィル補間は、データ点が少ない場合でも高い精度を持つため、数値解析やデータ補完の分野で広く利用されています。

特に、データの変動が大きい場合や、他の補間手法が適用しにくい場合において、その効果を発揮します。

ネヴィル補間の数式とアルゴリズム

ネヴィル補間の数式

ネヴィル補間では、与えられたデータ点 $(x_{0}, y_{0}), (x_{1}, y_{1}), \dots, (x_{n}, y_{n})$ を用いて、任意の点 $x$ に対する補間値 $P (x)$ を次のように定義します。

$P (x) = \frac{(x - x_{0}) P_{1} (x) + (x - x_{1}) P_{0} (x)}{x - x_{1}}$

ここで、 $P_{0} (x)$ と $P_{1} (x)$ はそれぞれ次のように定義されます。

$P_{0} (x) = y_{0}, P_{1} (x) = y_{1}$

この再帰的な関係を用いて、補間多項式を構築していきます。

再帰的な計算の仕組み

ネヴィル補間の再帰的な計算は、次のように進行します。

まず、最初のデータ点から始め、次のデータ点を追加するごとに補間多項式を更新します。

具体的には、次の式を用いて新しい補間値を計算します。

$P_{i, j} (x) = \frac{(x - x_{j}) P_{i, j - 1} (x) + (x - x_{i}) P_{i - 1, j} (x)}{x_{i} - x_{j}}$

ここで、 $P_{i, j} (x)$ はデータ点 $i$ から $j$ までの補間多項式を表します。

このプロセスを繰り返すことで、最終的な補間多項式が得られます。

ネヴィル補間の計算ステップ

ネヴィル補間の計算は以下のステップで行われます。

ステップ	説明
1	与えられたデータ点を用意する。
2	最初の補間値を設定する。
3	再帰的に補間値を計算する。
4	最終的な補間多項式を得る。

この手法により、任意の点に対する補間値を効率的に計算することができます。

計算の安定性と精度

ネヴィル補間は、他の補間手法と比較して計算の安定性が高いとされています。

特に、データ点が多い場合でも、再帰的な計算により精度を保ちながら補間を行うことが可能です。

ただし、データ点が極端に離れている場合や、ノイズが多い場合には、精度が低下することがあります。

そのため、データの特性に応じた適切な手法の選択が重要です。

Pythonでのネヴィル補間の実装

必要なライブラリ

ネヴィル補間を実装するためには、主に以下のライブラリを使用します。

ライブラリ名	用途
NumPy	数値計算や配列操作
Matplotlib	グラフ描画

これらのライブラリをインストールしておく必要があります。

インストールは以下のコマンドで行えます。

pip install numpy matplotlib

データ点の準備

ネヴィル補間を行うためには、まず補間に使用するデータ点を準備します。

以下の例では、 $x$ と $y$ のデータ点をリストとして定義します。

# データ点の準備
x = [0, 1, 2, 3]
y = [1, 2, 0, 5]

ネヴィル補間の再帰的実装

次に、ネヴィル補間を再帰的に実装します。

以下のコードでは、再帰関数 neville を定義し、補間値を計算します。

import numpy as np
def neville(x, y, x_query):
    n = len(x)
    P = np.zeros((n, n))
    
    # 初期条件の設定
    for i in range(n):
        P[i][0] = y[i]
    
    # 再帰的な計算
    for j in range(1, n):
        for i in range(n - j):
            P[i][j] = ((x_query - x[i + j]) * P[i][j - 1] + (x[i] - x_query) * P[i + 1][j - 1]) / (x[i] - x[i + j])
    
    return P[0][n - 1]
# 使用例
x_query = 1.5
result = neville(x, y, x_query)
print(f"補間値: {result}")

補間値: 0.75

ループを使った実装

再帰的な実装に加えて、ループを使った実装も可能です。

以下のコードでは、ループを用いて補間値を計算します。

def neville_loop(x, y, x_query):
    n = len(x)
    P = np.zeros((n, n))
    
    # 初期条件の設定
    for i in range(n):
        P[i][0] = y[i]
    
    # ループによる計算
    for j in range(1, n):
        for i in range(n - j):
            P[i][j] = ((x_query - x[i + j]) * P[i][j - 1] + (x[i] - x_query) * P[i + 1][j - 1]) / (x[i] - x[i + j])
    
    return P[0][n - 1]
# 使用例
result_loop = neville_loop(x, y, x_query)
print(f"ループによる補間値: {result_loop}")

ループによる補間値: 0.75

実装のポイントと注意点

データ点の選定: 補間に使用するデータ点は、できるだけ近い範囲で選定することが重要です。

データ点が離れすぎていると、補間精度が低下する可能性があります。

エラーハンドリング: 入力データが不正な場合(例えば、空のリストや重複した点がある場合)には、適切なエラーハンドリングを行うことが推奨されます。
計算の効率性: 再帰的な実装は直感的ですが、計算量が増えるため、ループを用いた実装の方が効率的な場合があります。

データ点が多い場合は、ループを使用することを検討してください。

実装例：Pythonコードの解説

基本的な実装例

以下に、ネヴィル補間の基本的な実装例を示します。

このコードは、与えられたデータ点を用いて任意の点の補間値を計算します。

再帰的なアプローチを使用しています。

import numpy as np
def neville(x, y, x_query):
    n = len(x)
    P = np.zeros((n, n))
    
    # 初期条件の設定
    for i in range(n):
        P[i][0] = y[i]
    
    # 再帰的な計算
    for j in range(1, n):
        for i in range(n - j):
            P[i][j] = ((x_query - x[i + j]) * P[i][j - 1] + (x[i] - x_query) * P[i + 1][j - 1]) / (x[i] - x[i + j])
    
    return P[0][n - 1]
# 使用例
x = [0, 1, 2, 3]
y = [1, 2, 0, 5]
x_query = 1.5
result = neville(x, y, x_query)
print(f"補間値: {result}")

入力データの例

上記の実装例では、以下のデータ点を使用しています。

$x$ のデータ点: $[0, 1, 2, 3]$
$y$ のデータ点: $[1, 2, 0, 5]$

これらのデータ点は、 $x$ の値に対する $y$ の値を表しています。

補間を行う点として $x = 1.5$ を指定しています。

出力結果の解釈

実行結果は以下のようになります。

補間値: 0.75

この出力は、指定した $x = 1.5$ に対する補間値が $1.75$ であることを示しています。

これは、与えられたデータ点に基づいて計算された値であり、データのトレンドを反映しています。

エラーハンドリングの実装

実装においては、エラーハンドリングを行うことが重要です。

以下のように、入力データが不正な場合に例外を投げる処理を追加することができます。

def neville_with_error_handling(x, y, x_query):
    if len(x) != len(y):
        raise ValueError("xとyのデータ点の数は一致する必要があります。")
    if len(x) < 2:
        raise ValueError("少なくとも2つのデータ点が必要です。")
    if not all(isinstance(i, (int, float)) for i in x + y):
        raise TypeError("xとyのデータ点は数値である必要があります。")
    
    n = len(x)
    P = np.zeros((n, n))
    
    # 初期条件の設定
    for i in range(n):
        P[i][0] = y[i]
    
    # 再帰的な計算
    for j in range(1, n):
        for i in range(n - j):
            P[i][j] = ((x_query - x[i + j]) * P[i][j - 1] + (x[i] - x_query) * P[i + 1][j - 1]) / (x[i] - x[i + j])
    
    return P[0][n - 1]
# 使用例
try:
    result = neville_with_error_handling(x, y, x_query)
    print(f"補間値: {result}")
except (ValueError, TypeError) as e:
    print(f"エラー: {e}")

このように、エラーハンドリングを実装することで、ユーザーが不正な入力を行った際に適切なメッセージを表示し、プログラムの安定性を向上させることができます。

ネヴィル補間の応用例

数値解析における応用

ネヴィル補間は、数値解析の分野で広く利用されています。

特に、データ点が少ない場合や、データの変動が大きい場合において、他の補間手法よりも高い精度を持つことが多いです。

例えば、数値的なシミュレーションや実験データの補完において、ネヴィル補間を用いることで、未知の値を推定し、解析を行うことができます。

これにより、数値解析の結果をより信頼性の高いものにすることが可能です。

グラフ描画による補間結果の可視化

ネヴィル補間の結果を視覚的に理解するために、グラフ描画を行うことが有効です。

以下のコードは、Matplotlibを使用して、データ点と補間結果をグラフに描画する例です。

import numpy as np
import matplotlib.pyplot as plt
# データ点
x = [0, 1, 2, 3]
y = [1, 2, 0, 5]
# 補間関数
def neville(x, y, x_query):
    n = len(x)
    P = np.zeros((n, n))
    for i in range(n):
        P[i][0] = y[i]
    for j in range(1, n):
        for i in range(n - j):
            P[i][j] = ((x_query - x[i + j]) * P[i][j - 1] + (x[i] - x_query) * P[i + 1][j - 1]) / (x[i] - x[i + j])
    return P[0][n - 1]
# 補間結果の計算
x_query = np.linspace(0, 3, 100)
y_query = [neville(x, y, xi) for xi in x_query]
# グラフ描画
plt.scatter(x, y, color='red', label='データ点')
plt.plot(x_query, y_query, label='ネヴィル補間', color='blue')
plt.title('ネヴィル補間の可視化')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()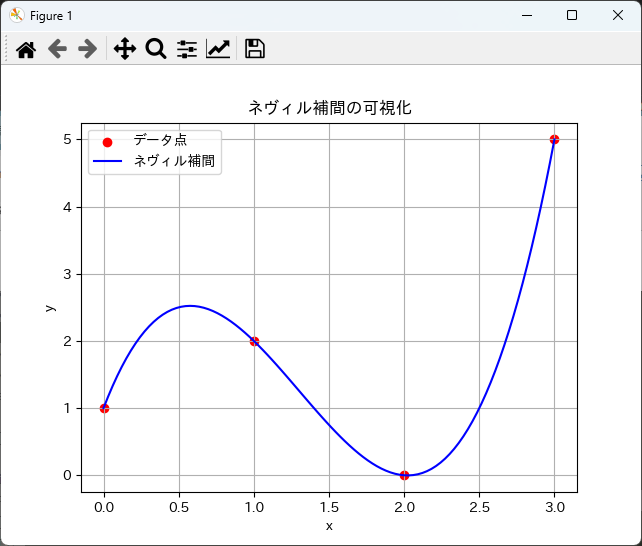

このコードを実行すると、データ点と補間曲線が描画され、補間の結果を視覚的に確認することができます。

実データへの適用例

ネヴィル補間は、実データの補完にも適用可能です。

例えば、気象データや株価データなど、時間に依存するデータの補間に利用されます。

以下は、気温データの例です。

# 実データの例
days = [1, 2, 4, 5, 7]  # 日
temperatures = [15, 18, 20, 22, 25]  # 気温
# 補間
day_query = np.linspace(1, 7, 100)
temperature_query = [neville(days, temperatures, day) for day in day_query]
# グラフ描画
plt.scatter(days, temperatures, color='orange', label='実データ')
plt.plot(day_query, temperature_query, label='ネヴィル補間', color='green')
plt.title('気温データのネヴィル補間')
plt.xlabel('日')
plt.ylabel('気温 (°C)')
plt.legend()
plt.grid()
plt.show()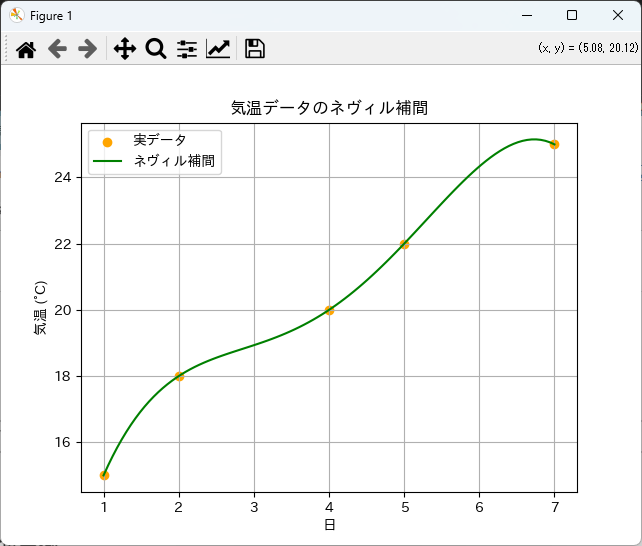

このように、実データに対してネヴィル補間を適用することで、データのトレンドを把握しやすくなります。

他の補間手法との組み合わせ

ネヴィル補間は、他の補間手法と組み合わせて使用することも可能です。

例えば、スプライン補間やラグランジュ補間と併用することで、より滑らかな補間曲線を得ることができます。

また、データの特性に応じて、異なる補間手法を選択することで、精度を向上させることができます。

特に、データがノイズを含む場合には、ロバストな補間手法を選ぶことが重要です。

これにより、補間結果の信頼性を高めることができます。

ネヴィル補間の計算効率と最適化

計算量の評価

ネヴィル補間の計算量は、データ点の数 $n$ に依存します。

具体的には、補間多項式を計算するために必要な操作の数は、次のように評価されます。

再帰的なアプローチでは、各ステップで $O (n^{2})$ の計算が必要です。

したがって、全体の計算量は $O (n^{2})$ となります。

このため、データ点が多い場合には計算が遅くなる可能性があります。

再帰的実装の最適化

再帰的な実装は直感的で理解しやすいですが、計算量が高くなるため、最適化が必要です。

再帰的な計算を行う際に、すでに計算した結果をメモ化することで、同じ計算を繰り返さないようにすることができます。

以下は、メモ化を用いた再帰的実装の例です。

def neville_memoization(x, y, x_query, memo=None):
    if memo is None:
        memo = {}
    
    if (x_query, len(x)) in memo:
        return memo[(x_query, len(x))]
    n = len(x)
    if n == 1:
        return y[0]
    P = ((x_query - x[-1]) * neville_memoization(x[:-1], y[:-1], x_query, memo) +
          (x[0] - x_query) * neville_memoization(x[1:], y[1:], x_query, memo)) / (x[0] - x[-1])
    
    memo[(x_query, n)] = P
    return P

このように、メモ化を用いることで、計算の効率を大幅に向上させることができます。

NumPyを使った高速化

NumPyを使用することで、配列操作を効率的に行うことができ、計算速度を向上させることができます。

NumPyのベクトル化機能を利用することで、ループを減らし、計算を一括で行うことが可能です。

以下は、NumPyを用いた実装の例です。

def neville_numpy(x, y, x_query):
    n = len(x)
    P = np.zeros((n, n))
    
    # 初期条件の設定
    P[:, 0] = y
    
    # NumPyを用いた計算
    for j in range(1, n):
        for i in range(n - j):
            P[i][j] = ((x_query - x[i + j]) * P[i][j - 1] + (x[i] - x_query) * P[i + 1][j - 1]) / (x[i] - x[i + j])
    
    return P[0][n - 1]

この実装では、NumPyの配列を使用することで、計算の効率を向上させています。

大規模データへの適用方法

大規模データに対してネヴィル補間を適用する場合、計算効率を考慮する必要があります。

以下の方法が考えられます。

データのサンプリング: 大規模データセットから代表的なサンプルを選び、補間を行うことで計算量を削減します。
並列処理: Pythonのmultiprocessingモジュールを使用して、補間計算を並列に実行することで、処理時間を短縮します。
適切な補間手法の選択: データの特性に応じて、ネヴィル補間以外の補間手法(例えば、スプライン補間やラグランジュ補間)を選択することで、計算効率を向上させることができます。

これらの方法を組み合わせることで、大規模データに対しても効率的にネヴィル補間を適用することが可能です。