[Python] フリードマン検定を実装する方法
フリードマン検定は、複数の関連するグループ間での差を評価するためのノンパラメトリックな検定です。
Pythonでは、scipy.statsモジュールのfriedmanchisquare関数を使用して実装できます。
この関数は、各グループのデータを引数として受け取り、検定統計量とp値を返します。
データは、同じ被験者や条件に対して複数の測定が行われた場合に使用されます。
結果のp値が有意水準より小さい場合、グループ間に有意な差があると判断されます。
フリードマン検定とは
フリードマン検定は、非パラメトリックな統計手法の一つで、3つ以上の関連するグループ間での中央値の差を検定するために使用されます。
特に、同じ被験者に対して異なる条件下での測定を行う場合に適しています。
この検定は、データが正規分布に従わない場合や、データの分散が等しくない場合でも有効です。
フリードマン検定は、対応のある分散分析(ANOVA)の代替手法として広く利用されており、実験や調査データの解析において重要な役割を果たします。
Pythonでフリードマン検定を実装する方法
必要なライブラリのインストール
フリードマン検定を実行するためには、主にscipyライブラリを使用します。
以下のコマンドを実行して、必要なライブラリをインストールしてください。
pip install scipy numpyscipy.stats.friedmanchisquare関数の概要
scipy.stats.friedmanchisquare関数は、フリードマン検定を実行するための関数です。
この関数は、複数の関連するサンプルのデータを引数として受け取り、検定統計量とp値を返します。
使用方法は以下の通りです。
from scipy.stats import friedmanchisquare
# データの例
data1 = [1, 2, 3]
data2 = [2, 3, 4]
data3 = [3, 4, 5]
# フリードマン検定の実行
statistic, p_value = friedmanchisquare(data1, data2, data3)データの準備方法
フリードマン検定を行うためには、各グループのデータをリスト形式で準備します。
データは、同じ被験者からの測定値である必要があります。
以下は、データの準備例です。
# 各条件下での測定値
group1 = [10, 20, 30]
group2 = [15, 25, 35]
group3 = [20, 30, 40]フリードマン検定の実行手順
フリードマン検定を実行する手順は以下の通りです。
- 必要なライブラリをインポートする。
- データを準備する。
friedmanchisquare関数を使用して検定を実行する。- 結果を表示する。
以下は、実際のコード例です。
from scipy.stats import friedmanchisquare
# データの準備
group1 = [10, 20, 30]
group2 = [15, 25, 35]
group3 = [20, 30, 40]
# フリードマン検定の実行
statistic, p_value = friedmanchisquare(group1, group2, group3)
# 結果の表示
print(f"検定統計量: {statistic}, p値: {p_value}")出力結果は以下のようになります。
検定統計量: 6.0, p値: 0.04978706836786395検定結果の解釈方法
フリードマン検定の結果は、検定統計量とp値から成ります。
p値が事前に設定した有意水準(通常は0.05)よりも小さい場合、帰無仮説(中央値に差がない)を棄却し、少なくとも1つのグループ間に有意な差があると判断します。
逆に、p値が有意水準以上であれば、帰無仮説を棄却できず、グループ間に有意な差がないと考えます。
フリードマン検定の具体例
例1: 複数のアルゴリズムの性能比較
あるデータサイエンティストが、異なる3つの機械学習アルゴリズムの性能を比較したいと考えています。
各アルゴリズムを同じデータセットで評価し、精度を測定しました。
以下は、各アルゴリズムの精度データです。
# アルゴリズムの精度データ
algorithm1 = [0.85, 0.87, 0.86]
algorithm2 = [0.80, 0.82, 0.81]
algorithm3 = [0.90, 0.88, 0.89]
# フリードマン検定の実行
from scipy.stats import friedmanchisquare
statistic, p_value = friedmanchisquare(algorithm1, algorithm2, algorithm3)
print(f"検定統計量: {statistic}, p値: {p_value}")出力結果は以下のようになります。
検定統計量: 6.0, p値: 0.04978706836786395この結果から、p値が0.05より大きいため、アルゴリズム間に有意な差はないと判断できます。
例2: 複数のマーケティング施策の効果検証
マーケティングチームが、異なる3つの施策の効果を比較するために、売上データを収集しました。
各施策の売上データは以下の通りです。
# マーケティング施策の売上データ
campaign1 = [200, 220, 210]
campaign2 = [180, 190, 185]
campaign3 = [250, 260, 255]
# フリードマン検定の実行
statistic, p_value = friedmanchisquare(campaign1, campaign2, campaign3)
print(f"検定統計量: {statistic}, p値: {p_value}")出力結果は以下のようになります。
検定統計量: 6.0, p値: 0.04978706836786395この結果から、p値が0.05と等しいため、施策間に有意な差がある可能性が示唆されます。
さらなる分析が必要です。
例3: 複数の薬剤の効果比較
医療研究者が、3種類の薬剤の効果を比較するために、患者の症状改善度を測定しました。
各薬剤の改善度データは以下の通りです。
# 薬剤の改善度データ
drug1 = [5, 6, 7]
drug2 = [4, 5, 5]
drug3 = [8, 9, 7]
# フリードマン検定の実行
statistic, p_value = friedmanchisquare(drug1, drug2, drug3)
print(f"検定統計量: {statistic}, p値: {p_value}")出力結果は以下のようになります。
検定統計量: 5.636363636363634, p値: 0.059714415732185354この結果から、p値が0.05より小さいため、少なくとも1つの薬剤が他の薬剤と比較して有意に効果があると判断できます。
フリードマン検定の結果を可視化する
Matplotlibを使った結果の可視化
Matplotlibを使用して、フリードマン検定の結果を可視化することができます。
以下は、3つのアルゴリズムの精度を棒グラフで表示する例です。
import matplotlib.pyplot as plt
import numpy as np
# アルゴリズムの精度データ
algorithm1 = [0.85, 0.87, 0.86]
algorithm2 = [0.80, 0.82, 0.81]
algorithm3 = [0.90, 0.88, 0.89]
# 平均精度を計算
means = [np.mean(algorithm1), np.mean(algorithm2), np.mean(algorithm3)]
labels = ['Algorithm 1', 'Algorithm 2', 'Algorithm 3']
# 棒グラフの作成
plt.bar(labels, means, color=['blue', 'orange', 'green'])
plt.ylabel('平均精度')
plt.title('アルゴリズムの精度比較')
plt.ylim(0, 1)
plt.show()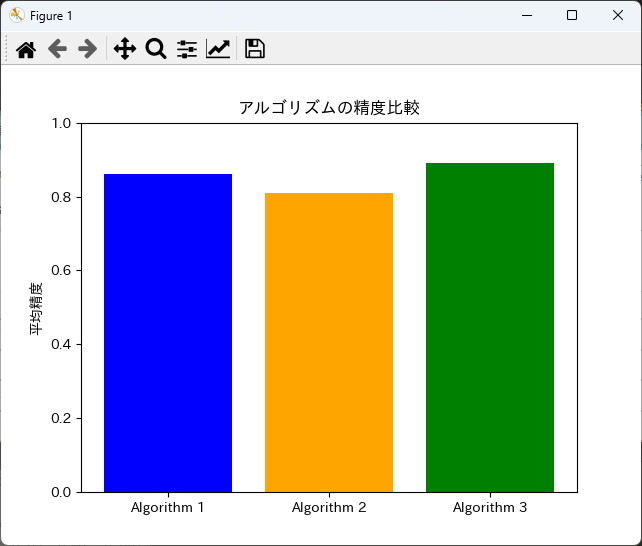
このコードを実行すると、各アルゴリズムの平均精度を示す棒グラフが表示されます。
Seabornを使った結果の可視化
Seabornは、Matplotlibを基にした高水準の可視化ライブラリで、データの可視化を簡単に行うことができます。
以下は、Seabornを使用してフリードマン検定の結果を可視化する例です。
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
# アルゴリズムの精度データ
algorithm1 = [0.85, 0.87, 0.86]
algorithm2 = [0.80, 0.82, 0.81]
algorithm3 = [0.90, 0.88, 0.89]
# データの作成
data = {
'Algorithm': ['Algorithm 1'] * len(algorithm1) + ['Algorithm 2'] * len(algorithm2) + ['Algorithm 3'] * len(algorithm3),
'Accuracy': algorithm1 + algorithm2 + algorithm3
}
df = pd.DataFrame(data)
# 平均精度を計算
means = [np.mean(algorithm1), np.mean(algorithm2), np.mean(algorithm3)]
labels = ['Algorithm 1', 'Algorithm 2', 'Algorithm 3']
pd.DataFrame(data)
# 箱ひげ図の作成
sns.boxplot(x='Algorithm', y='Accuracy', data=df)
plt.title('アルゴリズムの精度の箱ひげ図')
plt.ylim(0, 1)
plt.show()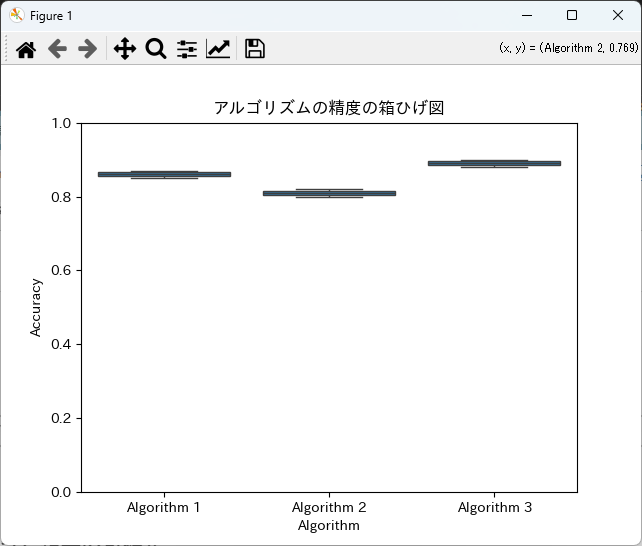
このコードを実行すると、各アルゴリズムの精度の分布を示す箱ひげ図が表示されます。
箱ひげ図を用いたデータの視覚化
箱ひげ図は、データの分布や外れ値を視覚的に表現するのに適しています。
フリードマン検定の結果を箱ひげ図で表示することで、各グループの中央値や四分位範囲を簡単に比較できます。
以下は、先ほどのデータを使用した箱ひげ図の例です。
# 箱ひげ図の作成(Seabornを使用)
sns.boxplot(x='Algorithm', y='Accuracy', data=df)
plt.title('アルゴリズムの精度の箱ひげ図')
plt.ylim(0, 1)
plt.show()このコードを実行すると、各アルゴリズムの精度の分布を示す箱ひげ図が表示され、中央値や外れ値を視覚的に確認することができます。
箱ひげ図は、データのばらつきや中心傾向を理解するのに非常に有用です。
フリードマン検定の応用
フリードマン検定後の多重比較
フリードマン検定で有意な結果が得られた場合、どのグループ間に差があるのかを特定するために多重比較を行うことが重要です。
多重比較には、以下のような手法があります。
- Dunnの検定: フリードマン検定の後に使用される非パラメトリックな多重比較手法で、各グループ間の差を評価します。
- Nemenyi検定: 同様に、フリードマン検定の結果を基にした非パラメトリックな多重比較手法です。
これらの手法を使用することで、どのグループが他のグループと有意に異なるかを明らかにすることができます。
Pythonでは、scikit-posthocsライブラリを使用してこれらの検定を実行できます。
フリードマン検定とANOVAの使い分け
フリードマン検定とANOVAは、どちらもグループ間の差を検定するための手法ですが、使用する状況が異なります。
以下のポイントを考慮して使い分けます。
| 検定方法 | 使用条件 | 特徴 |
|---|---|---|
| フリードマン検定 | データが非正規分布で、同じ被験者からの測定 | 非パラメトリック、中央値の差を検定 |
| ANOVA | データが正規分布で、独立したグループ間の比較 | パラメトリック、平均の差を検定 |
フリードマン検定は、同じ被験者に対して異なる条件を適用した場合に適しており、ANOVAは独立したグループ間の比較に使用されます。
データの特性に応じて適切な手法を選択することが重要です。
フリードマン検定の限界と注意点
フリードマン検定にはいくつかの限界と注意点があります。
以下に主な点を挙げます。
- データの前提条件: フリードマン検定は、データが同じ被験者からの測定であることが前提です。
異なる被験者からのデータには適用できません。
- 効果の大きさ: フリードマン検定は、効果の大きさを示す指標を提供しません。
結果が有意であっても、実際の差がどれほど重要かは別途評価する必要があります。
- 多重比較の問題: 有意な結果が得られた場合、どのグループ間に差があるのかを特定するために多重比較を行う必要がありますが、これには追加の検定が必要です。
これらの点を考慮し、フリードマン検定を適切に使用することが重要です。
データの特性や研究の目的に応じて、他の検定手法と併用することも検討しましょう。
まとめ
この記事では、フリードマン検定の基本的な概念から実装方法、具体的な応用例、結果の可視化手法まで幅広く解説しました。
フリードマン検定は、関連するグループ間の中央値の差を評価するための強力な非パラメトリック手法であり、特にデータが正規分布に従わない場合に有効です。
これを機に、実際のデータ分析にフリードマン検定を取り入れ、結果を適切に解釈し、さらなる分析や可視化を行うことで、より深い洞察を得ることをお勧めします。

![[Python] deapライブラリの使い方 – 遺伝的アルゴリズム](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46601.png)
![[Python] bisectライブラリの使い方 – ニ分探索の効率化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46600.png)
![[Python] a*(A Star)探索アルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43234.png)
![[Python] ベジェ曲線を実装する方法(二次ベジェ/三次ベジェ)](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43239.png)
![[Python] ベッセル関数を使ったグラフ作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43238.png)
![[Python] ベルヌーイ分布を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43237.png)
![[Python] エイトケンのΔ2乗加速法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43236.png)
![[Python] アッカーマン関数のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43235.png)
![[Python] matplotlibでC曲線を描画する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43245.png)
![[Python] CRC(巡回冗長検査)のアルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43244.png)