[Python] ベジェ曲線を実装する方法(二次ベジェ/三次ベジェ)
ベジェ曲線は、制御点を使って曲線を描く数学的手法です。
二次ベジェ曲線は3つの制御点、三次ベジェ曲線は4つの制御点を使用します。
Pythonでベジェ曲線を実装するには、制御点とパラメータ\(t\)(0から1の範囲)を使って曲線上の点を計算します。
二次ベジェ曲線は次の式で表されます:
\[B(t) = (1 – t)^2 P_0 + 2(1 – t)t P_1 + t^2 P_2\]
三次ベジェ曲線は次の式です:
\[B(t) = (1 – t)^3 P_0 + 3(1 – t)^2 t P_1 + 3(1 – t) t^2 P_2 + t^3 P_3\]
これらの式をPythonでループやリスト内包表記を使って実装できます。
ベジェ曲線とは
ベジェ曲線は、コンピュータグラフィックスやCAD(コンピュータ支援設計)で広く使用される数学的な曲線です。
特に、曲線の形状を制御するために「制御点」と呼ばれる点を使用します。
これにより、滑らかで自由な形状を描くことが可能になります。
ベジェ曲線には、二次ベジェ曲線と三次ベジェ曲線の2種類があり、それぞれ異なる数の制御点を持ちます。
二次ベジェ曲線は3つの制御点を使用し、三次ベジェ曲線は4つの制御点を使用します。
これらの曲線は、アニメーションやデザイン、ゲーム開発など、さまざまな分野で利用されています。
二次ベジェ曲線の実装
二次ベジェ曲線の数式
二次ベジェ曲線は、3つの制御点 \( P_0, P_1, P_2 \) を使用して定義されます。
曲線上の点 \( P(t) \) は、次の数式で表されます。
\[P(t) = (1 – t)^2 P_0 + 2(1 – t)t P_1 + t^2 P_2 \quad (0 \leq t \leq 1)\]
ここで、\( t \) は曲線上の位置を示すパラメータで、0から1の範囲で変化します。
Pythonでの二次ベジェ曲線の実装手順
- 制御点を定義する。
- 曲線上の点を計算する関数を作成する。
- 計算した点をリストに格納する。
- 曲線を描画するためのライブラリを使用する。
制御点を使った曲線の描画
以下は、二次ベジェ曲線を描画するためのPythonコードの例です。
import numpy as np
import matplotlib.pyplot as plt
# 制御点の定義
P0 = np.array([0, 0])
P1 = np.array([1, 2])
P2 = np.array([2, 0])
# 二次ベジェ曲線の計算
def bezier_quadratic(t, P0, P1, P2):
return (1 - t)**2 * P0 + 2 * (1 - t) * t * P1 + t**2 * P2
# 曲線上の点を計算
t_values = np.linspace(0, 1, 100)
curve_points = np.array([bezier_quadratic(t, P0, P1, P2) for t in t_values])
# 曲線の描画
plt.plot(curve_points[:, 0], curve_points[:, 1], label='二次ベジェ曲線')
plt.scatter(*zip(P0, P1, P2), color='red', label='制御点')
plt.legend()
plt.title('二次ベジェ曲線の描画')
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.grid()
plt.show()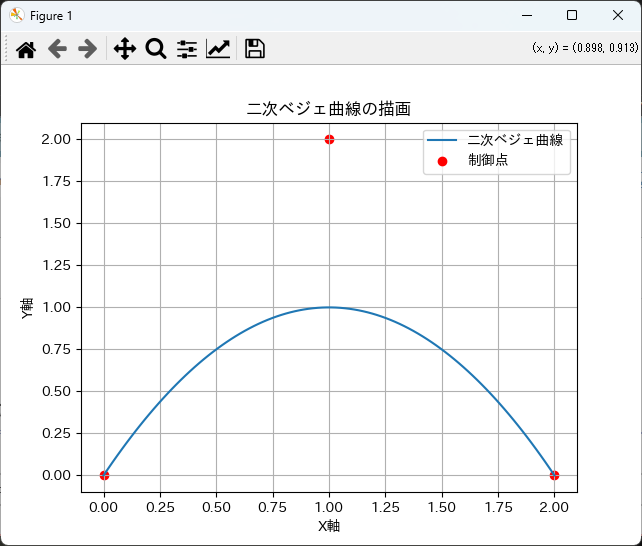
このコードを実行すると、二次ベジェ曲線とその制御点が描画されます。
Matplotlibを使った二次ベジェ曲線の可視化
上記のコードでは、Matplotlibを使用して二次ベジェ曲線を可視化しています。
plt.plot()関数を使って曲線を描画し、plt.scatter()関数で制御点を赤色で表示しています。
これにより、曲線の形状と制御点の位置を視覚的に確認することができます。
二次ベジェ曲線の応用例
二次ベジェ曲線は、以下のようなさまざまな応用があります。
| 応用分野 | 説明 |
|---|---|
| グラフィックデザイン | ロゴやアイコンの形状を滑らかに描くために使用される。 |
| アニメーション | キャラクターの動きやパスを滑らかにするために利用される。 |
| ゲーム開発 | キャラクターの移動経路やオブジェクトの形状を定義する。 |
これらの応用により、二次ベジェ曲線は多くのクリエイティブなプロジェクトで重要な役割を果たしています。
三次ベジェ曲線の実装
三次ベジェ曲線の数式
三次ベジェ曲線は、4つの制御点 \( P_0, P_1, P_2, P_3 \) を使用して定義されます。
曲線上の点 \( P(t) \) は、次の数式で表されます。
\[P(t) = (1 – t)^3 P_0 + 3(1 – t)^2 t P_1 + 3(1 – t) t^2 P_2 + t^3 P_3 \quad (0 \leq t \leq 1)\]
ここで、\( t \) は曲線上の位置を示すパラメータで、0から1の範囲で変化します。
Pythonでの三次ベジェ曲線の実装手順
- 制御点を定義する。
- 曲線上の点を計算する関数を作成する。
- 計算した点をリストに格納する。
- 曲線を描画するためのライブラリを使用する。
制御点を使った曲線の描画
以下は、三次ベジェ曲線を描画するためのPythonコードの例です。
import numpy as np
import matplotlib.pyplot as plt
# 制御点の定義
P0 = np.array([0, 0])
P1 = np.array([1, 2])
P2 = np.array([3, 1])
P3 = np.array([3, 0])
# 三次ベジェ曲線の計算
def bezier_cubic(t, P0, P1, P2, P3):
return (1 - t)**3 * P0 + 3 * (1 - t)**2 * t * P1 + 3 * (1 - t) * t**2 * P2 + t**3 * P3
# 曲線上の点を計算
t_values = np.linspace(0, 1, 100)
curve_points = np.array([bezier_cubic(t, P0, P1, P2, P3) for t in t_values])
# 曲線の描画
plt.plot(curve_points[:, 0], curve_points[:, 1], label='三次ベジェ曲線')
plt.scatter(*zip(P0, P1, P2, P3), color='red', label='制御点')
plt.legend()
plt.title('三次ベジェ曲線の描画')
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.grid()
plt.show()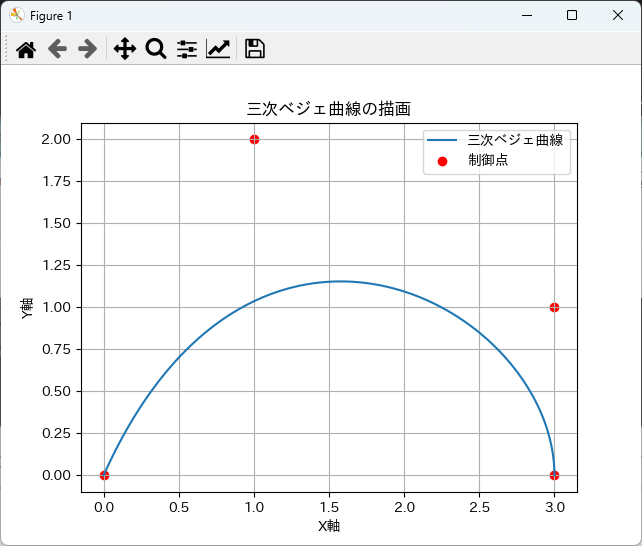
このコードを実行すると、三次ベジェ曲線とその制御点が描画されます。
Matplotlibを使った三次ベジェ曲線の可視化
上記のコードでは、Matplotlibを使用して三次ベジェ曲線を可視化しています。
plt.plot()関数を使って曲線を描画し、plt.scatter()関数で制御点を赤色で表示しています。
これにより、曲線の形状と制御点の位置を視覚的に確認することができます。
三次ベジェ曲線の応用例
三次ベジェ曲線は、以下のようなさまざまな応用があります。
| 応用分野 | 説明 |
|---|---|
| グラフィックデザイン | 複雑な形状や曲線を滑らかに描くために使用される。 |
| アニメーション | キャラクターの動きやカメラのパスを滑らかにするために利用される。 |
| ゲーム開発 | オブジェクトの移動経路やトラックの形状を定義する。 |
| CADソフトウェア | 精密な設計やモデリングにおいて、曲線を描くために使用される。 |
これらの応用により、三次ベジェ曲線は多くのクリエイティブなプロジェクトで重要な役割を果たしています。
ベジェ曲線の応用
グラフィックデザインにおけるベジェ曲線の利用
グラフィックデザインでは、ベジェ曲線が非常に重要な役割を果たしています。
特に、ロゴやアイコンのデザインにおいて、滑らかで自由な形状を描くために使用されます。
デザイナーは制御点を調整することで、曲線の形状を簡単に変更できるため、直感的にデザインを行うことが可能です。
また、ベジェ曲線はスケーラブルなベクター形式であるため、解像度に依存せず、どのサイズでも美しい形状を保つことができます。
アニメーションにおけるベジェ曲線の活用
アニメーションでは、キャラクターの動きやカメラのパスを滑らかにするためにベジェ曲線が利用されます。
アニメーターは、制御点を使って動きの軌道を定義し、自然な動きを実現します。
特に、イージング(加速・減速)効果を持たせるために、ベジェ曲線を用いて時間の経過に応じた動きの変化を表現することが一般的です。
これにより、アニメーションがよりリアルで魅力的になります。
ゲーム開発におけるベジェ曲線の応用
ゲーム開発においても、ベジェ曲線は重要な役割を果たしています。
キャラクターの移動経路やオブジェクトの形状を定義するために使用され、プレイヤーに対して滑らかな体験を提供します。
例えば、敵キャラクターのパスをベジェ曲線で設定することで、より自然な動きを実現できます。
また、レベルデザインにおいても、曲線を使って道や障害物の形状を作成することができます。
ベジェ曲線を使ったパスの生成
ベジェ曲線は、パスの生成にも広く利用されています。
特に、グラフィックソフトウェアやアニメーションツールでは、ユーザーが自由にパスを描くことができ、そのパスをベジェ曲線で表現します。
これにより、複雑な形状や動きを簡単に作成でき、デザインやアニメーションの効率が向上します。
さらに、パスをベジェ曲線で表現することで、後からの編集や調整が容易になります。
ベジェ曲線を使った物理シミュレーション
物理シミュレーションにおいても、ベジェ曲線は重要な役割を果たします。
特に、流体の動きや物体の軌道を滑らかに表現するために使用されます。
ベジェ曲線を用いることで、物体の動きがより自然に見えるようになり、リアルなシミュレーションが可能になります。
また、物理エンジンと組み合わせることで、動的な環境における物体の挙動をより正確に再現することができます。
ベジェ曲線の拡張
高次ベジェ曲線の実装
高次ベジェ曲線は、4つ以上の制御点を使用して定義される曲線です。
一般的に、\( n \) 次のベジェ曲線は \( n + 1 \) 個の制御点を持ち、次の数式で表されます。
\[P(t) = \sum_{i=0}^{n} B_{i,n}(t) P_i \quad (0 \leq t \leq 1)\]
ここで、\( B_{i,n}(t) \) はベルヌーイ多項式で、次のように定義されます。
\[B_{i,n}(t) = \binom{n}{i} (1 – t)^{n-i} t^i\]
Pythonでの高次ベジェ曲線の実装は、制御点のリストを受け取り、曲線上の点を計算する関数を作成することで行います。
複数のベジェ曲線をつなげる方法
複数のベジェ曲線をつなげるには、各曲線の終点と次の曲線の始点が一致するように制御点を設定します。
これにより、滑らかに接続された曲線を作成できます。
具体的には、次のように制御点を設定します。
- 曲線1の制御点: \( P_0, P_1, P_2 \)
- 曲線2の制御点: \( P_2, P_3, P_4 \)
この場合、\( P_2 \) が曲線1の終点であり、曲線2の始点となります。
これにより、2つの曲線が滑らかに接続されます。
ベジェ曲線とスプライン曲線の違い
ベジェ曲線とスプライン曲線は、どちらも滑らかな曲線を生成するために使用されますが、いくつかの違いがあります。
以下の表にその違いを示します。
| 特徴 | ベジェ曲線 | スプライン曲線 |
|---|---|---|
| 制御点の数 | 任意の数(通常は3または4) | 通常は3つ以上の制御点を持つ |
| 曲線の連続性 | 制御点の数に依存 | 各セグメントが連続的に接続される |
| 計算の複雑さ | 比較的簡単 | 複雑な計算が必要な場合がある |
| 使用例 | グラフィックデザイン、アニメーション | CAD、モデリング、アニメーション |
ベジェ曲線の最適化とパフォーマンス向上
ベジェ曲線の計算を最適化するためには、以下の方法が考えられます。
- キャッシング: 同じパラメータでの計算結果を保存し、再利用することで計算時間を短縮します。
- 分割統治法: 曲線を小さなセグメントに分割し、それぞれを独立に計算することで、全体の計算を効率化します。
- GPUを利用した描画: グラフィックス処理をGPUにオフロードすることで、描画性能を向上させます。
- 近似手法の使用: 高次のベジェ曲線を低次の曲線で近似することで、計算量を減らすことができます。
これらの最適化手法を適用することで、ベジェ曲線の描画や計算のパフォーマンスを向上させることが可能です。
まとめ
この記事では、ベジェ曲線の基本的な概念から、二次および三次ベジェ曲線の実装方法、さらにはその応用や拡張について詳しく解説しました。
ベジェ曲線は、グラフィックデザインやアニメーション、ゲーム開発など、さまざまな分野で重要な役割を果たしており、その特性を理解することで、より効果的なデザインや表現が可能になります。
これを機に、実際にベジェ曲線を使ったプロジェクトに取り組んでみることで、さらなるスキル向上を目指してみてはいかがでしょうか。

![[Python] deapライブラリの使い方 – 遺伝的アルゴリズム](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46601.png)
![[Python] bisectライブラリの使い方 – ニ分探索の効率化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46600.png)
![[Python] a*(A Star)探索アルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43234.png)
![[Python] ベッセル関数を使ったグラフ作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43238.png)
![[Python] ベルヌーイ分布を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43237.png)
![[Python] エイトケンのΔ2乗加速法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43236.png)
![[Python] アッカーマン関数のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43235.png)
![[Python] matplotlibでC曲線を描画する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43245.png)
![[Python] CRC(巡回冗長検査)のアルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43244.png)
![[Python] コラッツ予想(コラッツの問題)のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43243.png)
![[Python] コーシー分布の計算を行う方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43242.png)
![[Python] ボイヤームーア法で文字列検索する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43240.png)