[Python] シェルピンスキーの三角形を計算して描画する方法
シェルピンスキーの三角形は、再帰的に三角形を分割して作成されるフラクタル図形です。
Pythonでこれを描画するには、再帰関数を使って三角形を分割し、描画ライブラリ(例:matplotlibやturtle)を用います。
基本的な手順は、最初に大きな三角形を描き、その内部に小さな三角形を再帰的に描画していくことです。
再帰の深さを指定することで、フラクタルの細かさを調整できます。
シェルピンスキーの三角形とは
シェルピンスキーの三角形は、フラクタル幾何学の一例であり、自己相似性を持つ図形です。
最初は正三角形から始まり、その中に小さな正三角形を繰り返し配置することで形成されます。
このプロセスを繰り返すことで、無限に細かい構造を持つ三角形が生成されます。
シェルピンスキーの三角形は、数学的な美しさだけでなく、コンピュータサイエンスやアートの分野でも応用されており、再帰的なアルゴリズムやフラクタルの理解を深めるための良い教材となっています。
Pythonでシェルピンスキーの三角形を描画する準備
必要なライブラリのインストール
シェルピンスキーの三角形を描画するためには、主にmatplotlibとturtleという2つのライブラリを使用します。
これらのライブラリは、Pythonの標準ライブラリには含まれていないため、以下のコマンドを使用してインストールする必要があります。
pip install matplotlibmatplotlibの基本的な使い方
matplotlibは、Pythonでデータを可視化するための強力なライブラリです。
基本的な使い方は以下の通りです。
- ライブラリをインポートする
- データを準備する
- プロットを作成する
- 表示する
以下は、簡単な折れ線グラフを描画するサンプルコードです。
import matplotlib.pyplot as plt
# データの準備
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]
# プロットの作成
plt.plot(x, y)
# グラフの表示
plt.show()出力結果は、x軸とy軸にデータポイントがプロットされた折れ線グラフです。
turtleの基本的な使い方
turtleは、Pythonに組み込まれているグラフィックスライブラリで、簡単に図形を描画することができます。
基本的な使い方は以下の通りです。
- ライブラリをインポートする
- タートルを作成する
- 描画コマンドを実行する
- 描画を終了する
以下は、正方形を描画するサンプルコードです。
import turtle
# タートルの作成
t = turtle.Turtle()
# 正方形を描く
for _ in range(4):
t.forward(100) # 100ピクセル前進
t.right(90) # 90度右に回転
# 描画を終了
turtle.done()出力結果は、画面上に描かれた正方形です。
再帰関数の基礎知識
再帰関数とは、関数が自分自身を呼び出すことで問題を解決する手法です。
シェルピンスキーの三角形を描画する際には、再帰を利用して三角形を分割し、各部分を描画します。
再帰関数を設計する際には、以下の要素が重要です。
- 基本ケース: 再帰を終了する条件
- 再帰ケース: 自分自身を呼び出す条件
再帰関数を使うことで、複雑な問題をシンプルに解決することが可能になります。
シェルピンスキーの三角形を再帰的に計算する方法
再帰関数の設計
シェルピンスキーの三角形を描画するための再帰関数は、三角形を分割し、各部分を再帰的に描画するように設計します。
基本的な構造は以下のようになります。
def draw_sierpinski_triangle(t, order, size):
if order == 0:
# 基本ケース: 三角形を描く
for _ in range(3):
t.forward(size)
t.left(120)
else:
# 再帰ケース: 三角形を3つに分割
draw_sierpinski_triangle(t, order - 1, size / 2)
t.forward(size / 2)
draw_sierpinski_triangle(t, order - 1, size / 2)
t.backward(size / 2)
t.left(60)
t.forward(size / 2)
t.right(60)
draw_sierpinski_triangle(t, order - 1, size / 2)
t.left(60)
t.backward(size / 2)
t.right(60)この関数は、order(再帰の深さ)とsize(三角形のサイズ)を引数に取ります。
再帰的に三角形を描画するための基本的なロジックが含まれています。
三角形の頂点座標の計算
三角形の頂点座標は、描画する際に重要な要素です。
三角形の頂点は、以下のように計算できます。
- 頂点A: (x, y)
- 頂点B: (x + size, y)
- 頂点C: (x + size/2, y + (size * \(\frac{\sqrt{3}}{2}\)))
これにより、三角形の各頂点の位置を正確に指定することができます。
再帰的に描画する際には、これらの座標を基にして、次の三角形を描画します。
再帰の終了条件の設定
再帰関数には、必ず終了条件を設定する必要があります。
シェルピンスキーの三角形の場合、orderが0になったときに三角形を描画することが終了条件です。
これにより、無限に再帰が続くことを防ぎます。
具体的には、以下のように設定します。
if order == 0:
# 基本ケース: 三角形を描くこの条件が満たされると、三角形の描画が行われ、再帰が終了します。
再帰の深さによるフラクタルの細かさの調整
再帰の深さorderを調整することで、シェルピンスキーの三角形の細かさを変えることができます。
深さが大きいほど、より多くの三角形が描画され、複雑な形状になります。
逆に、深さが小さいと、シンプルな形状になります。
例えば、以下のように深さを変更して描画することができます。
# 再帰の深さを3に設定
draw_sierpinski_triangle(t, 3, 200)このように、再帰の深さを調整することで、シェルピンスキーの三角形の見た目を簡単に変えることができます。
matplotlibを使ったシェルピンスキーの三角形の描画
matplotlibでの三角形の描画方法
matplotlibを使用して三角形を描画するには、まず三角形の頂点座標を定義し、それをプロットする必要があります。
以下は、基本的な三角形を描画するサンプルコードです。
import matplotlib.pyplot as plt
# 三角形の頂点座標
triangle = [[0, 0], [1, 0], [0.5, (3**0.5)/2]]
# x座標とy座標を分ける
x, y = zip(*triangle + [triangle[0]]) # 最後に最初の点を追加して閉じる
# 三角形を描画
plt.fill(x, y, 'b') # 'b'は青色
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1)
plt.gca().set_aspect('equal')
plt.show()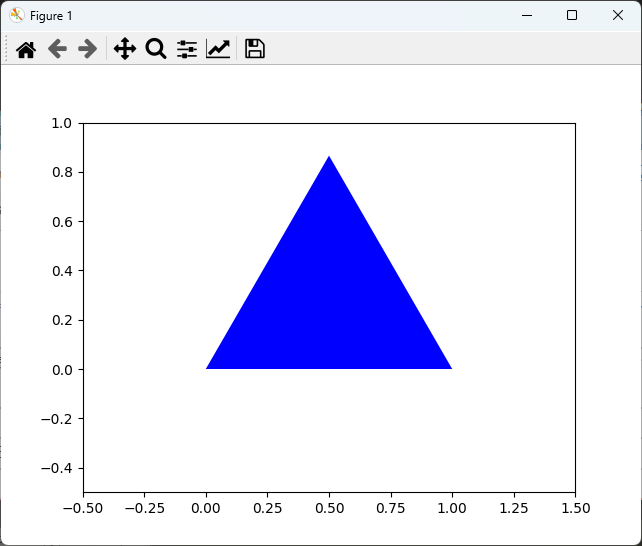
出力結果は、青色の正三角形が描画されたグラフです。
再帰的に三角形を描画する
再帰的にシェルピンスキーの三角形を描画するためには、先ほど設計した再帰関数をmatplotlibに適応させる必要があります。
以下は、再帰的に三角形を描画するサンプルコードです。
def draw_sierpinski_triangle(ax, order, vertices):
if order == 0:
# 三角形を描く
triangle = plt.Polygon(vertices, color='blue')
ax.add_patch(triangle)
else:
# 三角形を3つに分割
midpoints = [
[(vertices[0][0] + vertices[1][0]) / 2, (vertices[0][1] + vertices[1][1]) / 2],
[(vertices[1][0] + vertices[2][0]) / 2, (vertices[1][1] + vertices[2][1]) / 2],
[(vertices[2][0] + vertices[0][0]) / 2, (vertices[2][1] + vertices[0][1]) / 2]
]
draw_sierpinski_triangle(ax, order - 1, [vertices[0], midpoints[0], midpoints[2]])
draw_sierpinski_triangle(ax, order - 1, [midpoints[0], vertices[1], midpoints[1]])
draw_sierpinski_triangle(ax, order - 1, [midpoints[2], midpoints[1], vertices[2]])
# 描画の準備
fig, ax = plt.subplots()
ax.set_xlim(-0.5, 1.5)
ax.set_ylim(-0.5, 1.5)
ax.set_aspect('equal')
# 再帰的に三角形を描画
draw_sierpinski_triangle(ax, 3, [[0, 0], [1, 0], [0.5, (3**0.5)/2]])
plt.show()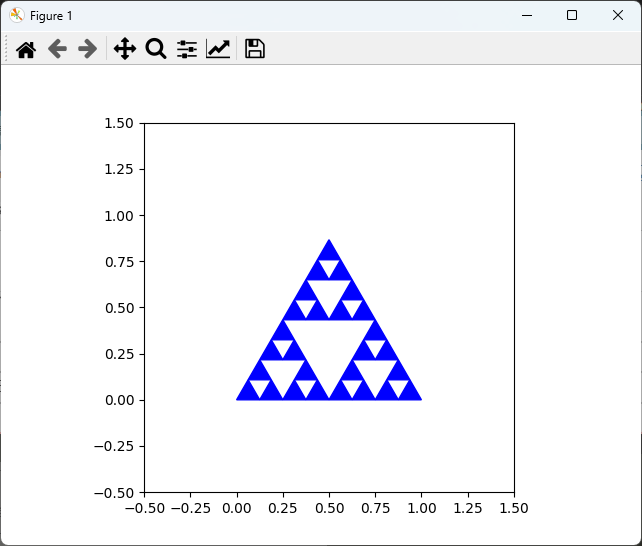
出力結果は、再帰的に描画されたシェルピンスキーの三角形です。
再帰の深さを変えてみる
再帰の深さを変更することで、描画されるシェルピンスキーの三角形の複雑さを調整できます。
例えば、draw_sierpinski_triangle(ax, 2, ...)とすることで、深さ2の三角形を描画できます。
深さを変えることで、以下のように描画結果が変わります。
# 再帰の深さを2に設定
draw_sierpinski_triangle(ax, 2, [[0, 0], [1, 0], [0.5, (3**0.5)/2]])
plt.show()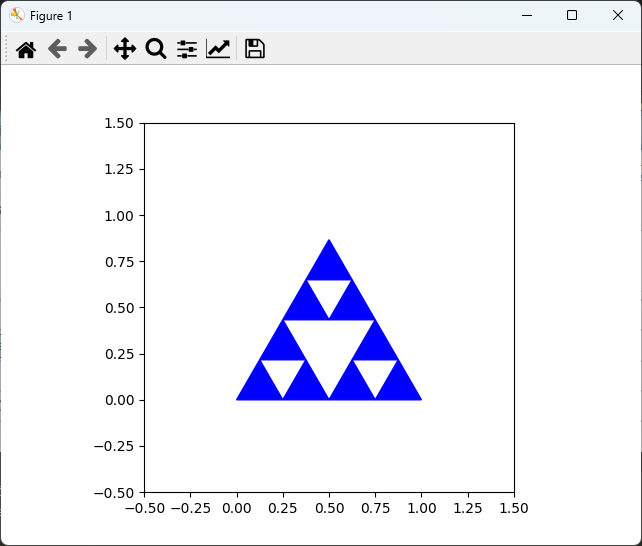
出力結果は、深さ2のシンプルなシェルピンスキーの三角形です。
色やスタイルのカスタマイズ
matplotlibでは、描画する三角形の色やスタイルを簡単にカスタマイズできます。
plt.Polygonのcolor引数を変更することで色を変えたり、edgecolor引数を使って枠線の色を指定したりできます。
以下は、色とスタイルをカスタマイズした例です。
def draw_sierpinski_triangle(ax, order, vertices):
if order == 0:
# 三角形を描く
triangle = plt.Polygon(vertices, color='red', edgecolor='black', linewidth=1.5)
ax.add_patch(triangle)
else:
# 三角形を3つに分割
midpoints = [
[(vertices[0][0] + vertices[1][0]) / 2, (vertices[0][1] + vertices[1][1]) / 2],
[(vertices[1][0] + vertices[2][0]) / 2, (vertices[1][1] + vertices[2][1]) / 2],
[(vertices[2][0] + vertices[0][0]) / 2, (vertices[2][1] + vertices[0][1]) / 2]
]
draw_sierpinski_triangle(ax, order - 1, [vertices[0], midpoints[0], midpoints[2]])
draw_sierpinski_triangle(ax, order - 1, [midpoints[0], vertices[1], midpoints[1]])
draw_sierpinski_triangle(ax, order - 1, [midpoints[2], midpoints[1], vertices[2]])
# 描画の準備
fig, ax = plt.subplots()
ax.set_xlim(-0.5, 1.5)
ax.set_ylim(-0.5, 1.5)
ax.set_aspect('equal')
# 再帰的に三角形を描画
draw_sierpinski_triangle(ax, 3, [[0, 0], [1, 0], [0.5, (3**0.5)/2]])
plt.show()出力結果は、赤色の三角形に黒い枠線が描かれたシェルピンスキーの三角形です。
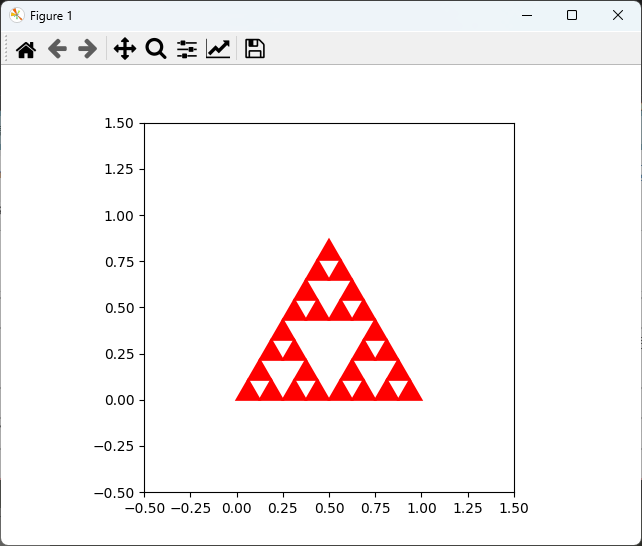
このように、色やスタイルを変更することで、視覚的に魅力的なフラクタルを作成することができます。
turtleを使ったシェルピンスキーの三角形の描画
turtleでの三角形の描画方法
turtleライブラリを使用して三角形を描画するには、タートルを動かして三角形の各辺を描く必要があります。
以下は、基本的な三角形を描画するサンプルコードです。
import turtle
# タートルの設定
t = turtle.Turtle()
# 三角形を描く関数
def draw_triangle(size):
for _ in range(3):
t.forward(size) # 指定したサイズだけ前進
t.left(120) # 120度左に回転
# 三角形を描画
draw_triangle(100)
# 描画を終了
turtle.done()
出力結果は、画面上に描かれた正三角形です。
再帰的に三角形を描画する
再帰的にシェルピンスキーの三角形を描画するためには、先ほど設計した再帰関数をturtleに適応させる必要があります。
以下は、再帰的に三角形を描画するサンプルコードです。
def draw_sierpinski_triangle(t, order, size):
if order == 0:
draw_triangle(size) # 基本ケース: 三角形を描く
else:
# 再帰ケース: 三角形を3つに分割
draw_sierpinski_triangle(t, order - 1, size / 2)
t.forward(size / 2)
draw_sierpinski_triangle(t, order - 1, size / 2)
t.backward(size / 2)
t.left(60)
t.forward(size / 2)
t.right(60)
draw_sierpinski_triangle(t, order - 1, size / 2)
t.left(60)
t.backward(size / 2)
t.right(60)
# タートルの設定
t = turtle.Turtle()
t.speed(0) # 最速で描画
# 再帰的に三角形を描画
draw_sierpinski_triangle(t, 3, 200)
# 描画を終了
turtle.done()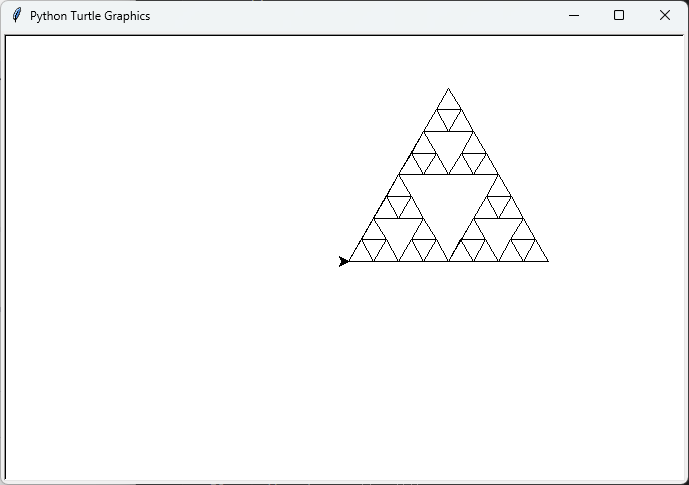
出力結果は、再帰的に描画されたシェルピンスキーの三角形です。
再帰の深さを変えてみる
再帰の深さを変更することで、描画されるシェルピンスキーの三角形の複雑さを調整できます。
例えば、draw_sierpinski_triangle(t, 2, 200)とすることで、深さ2の三角形を描画できます。
深さを変えることで、以下のように描画結果が変わります。
# 再帰の深さを2に設定
draw_sierpinski_triangle(t, 2, 200)
# 描画を終了
turtle.done()出力結果は、深さ2のシンプルなシェルピンスキーの三角形です。
アニメーションとしての描画
turtleライブラリの特徴の一つは、描画過程をアニメーションとして視覚化できることです。
タートルの動きを遅くすることで、描画の過程を観察することができます。
以下は、アニメーションとして描画するサンプルコードです。
def draw_sierpinski_triangle(t, order, size):
if order == 0:
draw_triangle(size) # 基本ケース: 三角形を描く
else:
# 再帰ケース: 三角形を3つに分割
draw_sierpinski_triangle(t, order - 1, size / 2)
t.forward(size / 2)
draw_sierpinski_triangle(t, order - 1, size / 2)
t.backward(size / 2)
t.left(60)
t.forward(size / 2)
t.right(60)
draw_sierpinski_triangle(t, order - 1, size / 2)
t.left(60)
t.backward(size / 2)
t.right(60)
# タートルの設定
t = turtle.Turtle()
t.speed(1) # 描画速度を遅くする
# 再帰的に三角形を描画
draw_sierpinski_triangle(t, 3, 200)
# 描画を終了
turtle.done()出力結果は、アニメーションとして描画されるシェルピンスキーの三角形です。
描画過程を観察することで、再帰的な構造がどのように形成されるかを理解することができます。
シェルピンスキーの三角形の応用例
3Dシェルピンスキーのピラミッドの描画
シェルピンスキーの三角形を3次元に拡張すると、シェルピンスキーのピラミッドが得られます。
これは、正四面体を基にしたフラクタルで、各面を再帰的に分割していくことで形成されます。
Pythonでは、matplotlibの3Dプロット機能を使用して描画できます。
以下は、3Dシェルピンスキーのピラミッドを描画するサンプルコードです。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
def draw_sierpinski_pyramid(ax, order, vertices):
if order == 0:
# 基本ケース: 四面体を描く
ax.add_collection3d(Poly3DCollection([vertices], color='cyan', linewidths=1, edgecolors='r', alpha=.25))
else:
midpoints = [
[(vertices[0][0] + vertices[1][0]) / 2, (vertices[0][1] + vertices[1][1]) / 2, (vertices[0][2] + vertices[1][2]) / 2],
[(vertices[1][0] + vertices[2][0]) / 2, (vertices[1][1] + vertices[2][1]) / 2, (vertices[1][2] + vertices[2][2]) / 2],
[(vertices[2][0] + vertices[0][0]) / 2, (vertices[2][1] + vertices[0][1]) / 2, (vertices[2][2] + vertices[0][2]) / 2],
[(vertices[0][0] + vertices[3][0]) / 2, (vertices[0][1] + vertices[3][1]) / 2, (vertices[0][2] + vertices[3][2]) / 2],
[(vertices[1][0] + vertices[3][0]) / 2, (vertices[1][1] + vertices[3][1]) / 2, (vertices[1][2] + vertices[3][2]) / 2],
[(vertices[2][0] + vertices[3][0]) / 2, (vertices[2][1] + vertices[3][1]) / 2, (vertices[2][2] + vertices[3][2]) / 2],
]
draw_sierpinski_pyramid(ax, order - 1, [vertices[0], midpoints[0], midpoints[2], midpoints[3]])
draw_sierpinski_pyramid(ax, order - 1, [midpoints[0], vertices[1], midpoints[1], midpoints[4]])
draw_sierpinski_pyramid(ax, order - 1, [midpoints[2], midpoints[1], vertices[2], midpoints[5]])
draw_sierpinski_pyramid(ax, order - 1, [midpoints[3], midpoints[4], midpoints[5], vertices[3]])
# 3Dプロットの準備
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_box_aspect([1,1,1]) # アスペクト比を設定
# 四面体の頂点
vertices = [[0, 0, 0], [1, 0, 0], [0.5, 0.5 * (3**0.5), 0], [0.5, 0.5 / (3**0.5), 1]]
# 再帰的にピラミッドを描画
draw_sierpinski_pyramid(ax, 2, vertices)
plt.show()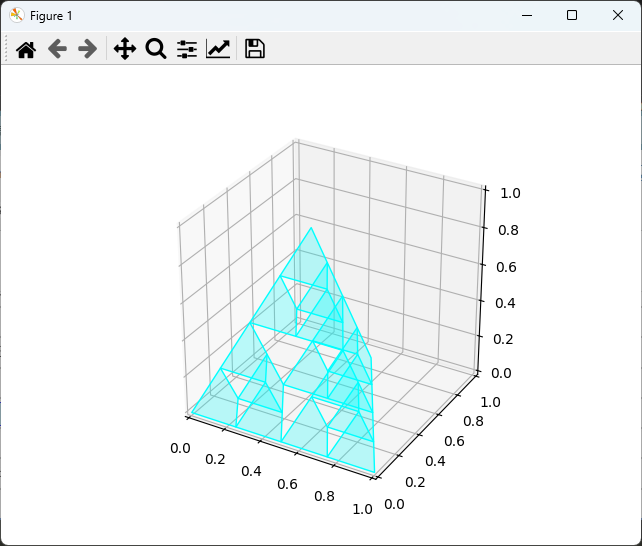
出力結果は、3Dのシェルピンスキーのピラミッドです。
シェルピンスキーのカーペットの描画
シェルピンスキーのカーペットは、2次元のフラクタルで、正方形を再帰的に分割していくことで形成されます。
以下は、シェルピンスキーのカーペットを描画するサンプルコードです。
def draw_sierpinski_carpet(t, order, size):
if order == 0:
for _ in range(4):
t.forward(size)
t.right(90)
else:
for i in range(3):
for j in range(3):
if (i, j) != (1, 1): # 中央の正方形を描かない
t.penup()
t.goto(i * size / 3, j * size / 3)
t.pendown()
draw_sierpinski_carpet(t, order - 1, size / 3)
# タートルの設定
t = turtle.Turtle()
t.speed(0) # 最速で描画
# 再帰的にカーペットを描画
draw_sierpinski_carpet(t, 3, 300)
# 描画を終了
turtle.done()出力結果は、シェルピンスキーのカーペットが描画されたものです。
シェルピンスキーの三角形を使ったアート作品
シェルピンスキーの三角形は、アート作品にも多く利用されています。
フラクタルの特性を活かして、複雑で美しいパターンを作成することができます。
例えば、色を変えたり、異なるサイズの三角形を組み合わせたりすることで、視覚的に魅力的な作品を作ることができます。
以下は、色を変えたシェルピンスキーの三角形を描画するサンプルコードです。
def draw_colored_sierpinski_triangle(t, order, size, color):
if order == 0:
t.fillcolor(color)
t.begin_fill()
draw_triangle(size)
t.end_fill()
else:
draw_colored_sierpinski_triangle(t, order - 1, size / 2, 'red')
t.forward(size / 2)
draw_colored_sierpinski_triangle(t, order - 1, size / 2, 'green')
t.backward(size / 2)
t.left(60)
t.forward(size / 2)
t.right(60)
draw_colored_sierpinski_triangle(t, order - 1, size / 2, 'blue')
t.left(60)
t.backward(size / 2)
t.right(60)
# タートルの設定
t = turtle.Turtle()
t.speed(0) # 最速で描画
# 再帰的に色付きの三角形を描画
draw_colored_sierpinski_triangle(t, 3, 200, 'yellow')
# 描画を終了
turtle.done()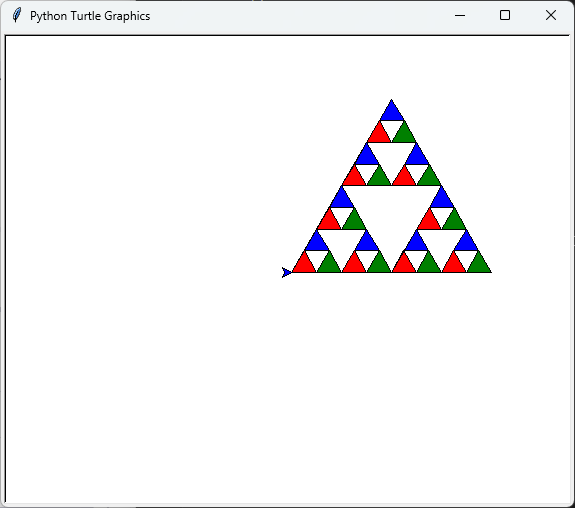
出力結果は、色とりどりのシェルピンスキーの三角形です。
シェルピンスキーの三角形を使ったゲームデザイン
シェルピンスキーの三角形は、ゲームデザインにも応用されています。
フラクタルの特性を利用して、レベルデザインや背景アートを作成することができます。
例えば、シェルピンスキーの三角形を背景に使用することで、視覚的に印象的なゲーム環境を作ることができます。
また、フラクタルの特性を持つキャラクターやオブジェクトをデザインすることも可能です。
以下は、シェルピンスキーの三角形を背景にしたゲームの簡単なアイデアです。
- レベルデザイン: シェルピンスキーの三角形を基にした迷路やパズルを作成し、プレイヤーがその中を探索するゲーム。
- 背景アート: ゲームの背景にシェルピンスキーの三角形を使用し、動的に色を変化させることで、視覚的に魅力的な環境を提供。
- キャラクター: フラクタルの特性を持つキャラクターをデザインし、プレイヤーがそのキャラクターを操作して冒険するゲーム。
このように、シェルピンスキーの三角形は、アートやゲームデザインにおいても多くの可能性を秘めています。
まとめ
この記事では、シェルピンスキーの三角形の基本的な概念から、Pythonを使った描画方法、さらには応用例まで幅広く取り上げました。
シェルピンスキーの三角形は、再帰的な構造を持つフラクタルであり、さまざまなプログラミング手法を通じて視覚的に表現することが可能です。
これを機に、シェルピンスキーの三角形を使ったプロジェクトやアート作品に挑戦してみると、新たな発見や創造性を引き出すことができるでしょう。

![[Python] deapライブラリの使い方 – 遺伝的アルゴリズム](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46601.png)
![[Python] bisectライブラリの使い方 – ニ分探索の効率化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46600.png)
![[Python] a*(A Star)探索アルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43234.png)
![[Python] ベジェ曲線を実装する方法(二次ベジェ/三次ベジェ)](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43239.png)
![[Python] ベッセル関数を使ったグラフ作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43238.png)
![[Python] ベルヌーイ分布を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43237.png)
![[Python] エイトケンのΔ2乗加速法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43236.png)
![[Python] アッカーマン関数のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43235.png)
![[Python] matplotlibでC曲線を描画する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43245.png)
![[Python] CRC(巡回冗長検査)のアルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43244.png)
![[Python] コラッツ予想(コラッツの問題)のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43243.png)
![[Python] コーシー分布の計算を行う方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43242.png)