[Python] matplotlibでリサージュ曲線を描く方法

matplotlibを使用してリサージュ曲線を描くには、まずnumpyで時間の配列を作成し、次にsin関数を使ってx軸とy軸の座標を計算します。

リサージュ曲線は、2つの異なる周波数の正弦波をx軸とy軸にプロットすることで得られます。

例えば、x座標は$\sin (a\cdot t)$、y座標は$\sin (b\cdot t+\delta )$の形で表され、ここで$a$と$b$は周波数、$\delta$は位相差です。

最後にmatplotlib.pyplot.plot()でプロットします。

リサージュ曲線の描画を通じて、データ可視化の楽しさを体験し、さまざまなパラメータを試してみることをお勧めします。

リサージュ曲線とは

リサージュ曲線は、2つの異なる周波数の正弦波が重なり合うことで形成される美しい曲線です。

この曲線は、物理学や工学の分野で振動や波動の解析に利用されることが多く、特に振動子や振動システムの挙動を視覚的に理解するために役立ちます。

リサージュ曲線は、周波数比や位相差を変えることで多様な形状を描くことができ、アートやデザインの分野でも注目されています。

Pythonのmatplotlibライブラリを使用することで、簡単にリサージュ曲線を描画することが可能です。

matplotlibの基本

matplotlibとは

matplotlibは、Pythonでデータを可視化するための強力なライブラリです。

2Dおよび3Dのグラフを描画する機能を提供し、科学技術計算やデータ分析の分野で広く利用されています。

特に、データのトレンドやパターンを視覚的に表現するために非常に便利です。

matplotlibを使用することで、簡単に高品質なグラフを作成することができます。

matplotlibのインストール方法

matplotlibは、Pythonのパッケージ管理ツールであるpipを使用して簡単にインストールできます。

以下のコマンドを実行することでインストールが可能です。

pip install matplotlib

インストールが完了したら、Pythonのスクリプトやインタラクティブな環境でmatplotlibを使用することができます。

matplotlibの基本的な使い方

matplotlibを使用する際は、まずライブラリをインポートする必要があります。

一般的には以下のようにインポートします。

import matplotlib.pyplot as plt

このインポートにより、pltというエイリアスを使ってmatplotlibの機能にアクセスできます。

基本的なグラフを描画するためには、データを用意し、plt.plot()関数を使用します。

グラフ描画の基本構文

matplotlibでグラフを描画する基本的な構文は以下の通りです。

import matplotlib.pyplot as plt
# データの準備
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]
# グラフの描画
plt.plot(x, y)
# 軸ラベルとタイトルの設定
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.title('基本的なグラフ')
# グラフの表示
plt.show()

このコードを実行すると、指定したデータに基づいてグラフが表示されます。

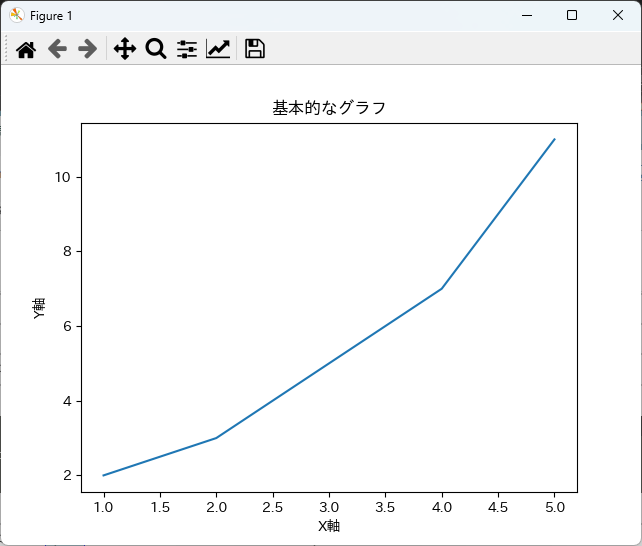
plt.show()を呼び出すことで、描画したグラフをウィンドウに表示することができます。

numpyを使ったデータ生成

numpyとは

numpyは、Pythonで数値計算を行うためのライブラリで、特に多次元配列(ndarray)を効率的に扱うことができます。

科学技術計算やデータ分析において、数値データの操作や計算を高速に行うための機能が豊富に用意されています。

numpyを使用することで、行列演算や統計計算、FFT(高速フーリエ変換)などが簡単に実行できます。

numpyのインストール方法

numpyはpipを使用して簡単にインストールできます。

以下のコマンドを実行することでインストールが可能です。

pip install numpy

インストールが完了したら、Pythonのスクリプトやインタラクティブな環境でnumpyを使用することができます。

numpyでの配列生成

numpyを使用して配列を生成するには、numpy.array()関数を使います。

以下は、リストからnumpy配列を生成する例です。

import numpy as np
# リストからnumpy配列を生成
data = [1, 2, 3, 4, 5]
array = np.array(data)
print(array)

このコードを実行すると、リストがnumpy配列に変換され、出力は以下のようになります。

[1 2 3 4 5]

numpyのsin関数を使ったデータ生成

numpyには、三角関数を計算するための便利な関数が用意されています。

特に、numpy.sin()関数を使用することで、角度の配列に対する正弦の値を簡単に計算できます。

以下は、0から2πまでの範囲で正弦波を生成する例です。

import numpy as np
# 0から2πまでの100点を生成
x = np.linspace(0, 2 * np.pi, 100)
# 正弦波の計算
y = np.sin(x)
print(y)

このコードを実行すると、0から2πまでの100点に対する正弦の値が出力されます。

出力の一部は以下のようになります。

[ 0.          0.06342392  0.12659245  0.18925124  0.25114799 ...]

このように、numpyを使用することで、効率的にデータを生成し、数値計算を行うことができます。

リサージュ曲線を描くための準備

リサージュ曲線のパラメータ設定

リサージュ曲線を描くためには、いくつかのパラメータを設定する必要があります。

主に、周波数と位相差が重要な役割を果たします。

周波数$a$と$b$の設定

リサージュ曲線の形状は、2つの異なる周波数$a$と$b$によって決まります。

これらの周波数は、x軸とy軸に沿った正弦波の振動数を表します。

周波数の比率を変えることで、さまざまな形状のリサージュ曲線を生成できます。

# 周波数の設定
a = 5  # x軸の周波数
b = 3  # y軸の周波数

位相差$\delta$の設定

位相差$\delta$は、x軸とy軸の波の位相のずれを表します。

この値を変更することで、リサージュ曲線の形状が変化します。

位相差はラジアンで指定します。

# 位相差の設定
delta = np.pi / 2  # 90度の位相差

時間配列の生成

リサージュ曲線を描くためには、時間の配列を生成する必要があります。

numpyのlinspace関数を使用して、一定の間隔で時間の値を生成します。

# 時間配列の生成
t = np.linspace(0, 2 * np.pi, 1000)  # 0から2πまでの1000点

x座標とy座標の計算

リサージュ曲線のx座標とy座標は、設定した周波数と位相差を用いて計算します。

以下の式を使用して、x座標とy座標を求めます。

$$x=a\cdot \sin (at)$$

$$y=b\cdot \sin (bt+\delta )$$

これをPythonで実装すると、次のようになります。

# x座標とy座標の計算
x = a * np.sin(a * t)  # x座標
y = b * np.sin(b * t + delta)  # y座標

このようにして、リサージュ曲線を描くための準備が整いました。

次のステップでは、これらの座標を用いて実際にリサージュ曲線を描画します。

matplotlibでリサージュ曲線を描く

matplotlibでのプロット方法

リサージュ曲線を描くためには、まずmatplotlibをインポートし、先ほど計算したx座標とy座標を用いてプロットします。

以下のコードでは、plt.plot()関数を使用してリサージュ曲線を描画します。

import numpy as np
import matplotlib.pyplot as plt
# リサージュ曲線のパラメータ設定
a = 5  # x軸の周波数
b = 3  # y軸の周波数
delta = np.pi / 2  # 位相差
# 時間配列の生成
t = np.linspace(0, 2 * np.pi, 1000)
# x座標とy座標の計算
x = a * np.sin(a * t)
y = b * np.sin(b * t + delta)
# リサージュ曲線のプロット
plt.plot(x, y)

軸ラベルとタイトルの追加

グラフに軸ラベルとタイトルを追加することで、視覚的にわかりやすくなります。

plt.xlabel()とplt.ylabel()を使用して軸ラベルを設定し、plt.title()でタイトルを追加します。

# 軸ラベルとタイトルの追加
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.title('リサージュ曲線')

グリッドの追加

グラフにグリッドを追加することで、データの読み取りが容易になります。

plt.grid()を使用してグリッドを表示します。

# グリッドの追加
plt.grid(True)

グラフの保存方法

描画したグラフを画像ファイルとして保存するには、plt.savefig()関数を使用します。

ファイル名と形式を指定することで、PNGやJPEGなどの形式で保存できます。

# グラフの保存方法
plt.savefig('lisajous_curve.png')  # PNG形式で保存

最後に、plt.show()を呼び出してグラフを表示します。

# グラフの表示
plt.show()

これで、リサージュ曲線を描画し、必要な情報をグラフに追加する準備が整いました。

全体のコードは以下のようになります。

import numpy as np
import matplotlib.pyplot as plt
# リサージュ曲線のパラメータ設定
a = 5
b = 3
delta = np.pi / 2
# 時間配列の生成
t = np.linspace(0, 2 * np.pi, 1000)
# x座標とy座標の計算
x = a * np.sin(a * t)
y = b * np.sin(b * t + delta)
# リサージュ曲線のプロット
plt.plot(x, y)
# 軸ラベルとタイトルの追加
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.title('リサージュ曲線')
# グリッドの追加
plt.grid(True)
# グラフの保存方法
plt.savefig('lisajous_curve.png')
# グラフの表示
plt.show()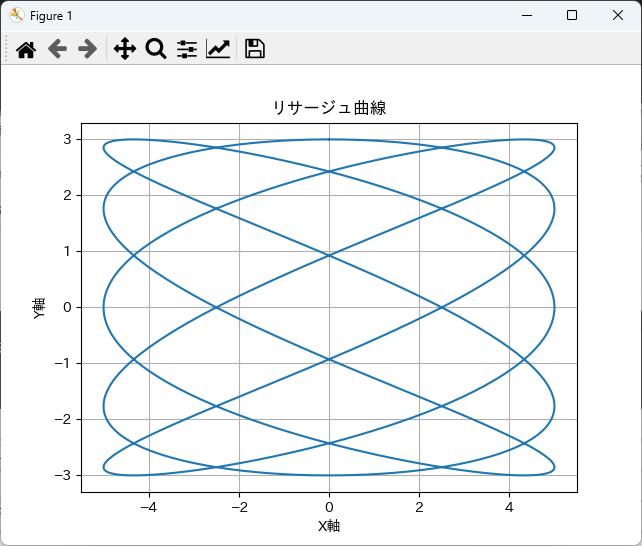

このコードを実行することで、リサージュ曲線が描画され、指定したファイル名で保存されます。

リサージュ曲線の応用例

リサージュ曲線は、さまざまなパラメータを変更することで多様な形状を描くことができ、さまざまな応用が可能です。

以下にいくつかの応用例を紹介します。

周波数比を変えたリサージュ曲線

周波数比を変えることで、リサージュ曲線の形状が大きく変わります。

例えば、周波数比が1:1の場合は円形に近い形状になりますが、比が異なると複雑なパターンが生成されます。

# 周波数比を変えたリサージュ曲線の例
a = 3  # x軸の周波数
b = 2  # y軸の周波数

この設定でリサージュ曲線を描くと、特有の美しいパターンが得られます。

位相差を変えたリサージュ曲線

位相差を変更することで、リサージュ曲線の形状が変化します。

位相差が0の場合、2つの波は同じ位相で振動しますが、90度($\frac{\pi }{2}$ラジアン)の位相差を持つと、より複雑な形状が生成されます。

# 位相差を変えたリサージュ曲線の例
delta = np.pi / 4  # 45度の位相差

この設定で描画すると、異なる形状のリサージュ曲線が得られます。

アニメーションで動的にリサージュ曲線を描く

matplotlibのFuncAnimationを使用することで、リサージュ曲線を動的に描画するアニメーションを作成できます。

時間の経過に伴って曲線が描かれる様子を視覚的に楽しむことができます。

from matplotlib.animation import FuncAnimation
# アニメーションの設定
fig, ax = plt.subplots()
line, = ax.plot([], [], lw=2)
def init():
    ax.set_xlim(-a, a)
    ax.set_ylim(-b, b)
    return line,
def update(frame):
    x = a * np.sin(a * frame)
    y = b * np.sin(b * frame + delta)
    line.set_data(x, y)
    return line,
ani = FuncAnimation(fig, update, frames=np.linspace(0, 2 * np.pi, 100), init_func=init, blit=True)
plt.show()

このコードを実行すると、リサージュ曲線が時間とともに動的に描画されます。

3Dリサージュ曲線の描画

リサージュ曲線は3次元空間でも描画することができます。

3Dプロットを使用することで、より立体的な視覚効果を得ることができます。

from mpl_toolkits.mplot3d import Axes3D
# 3Dプロットの設定
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# z座標の計算
z = np.sin(t)
# 3Dリサージュ曲線の描画
ax.plot(x, y, z)
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')
plt.title('3Dリサージュ曲線')
plt.show()

このコードを実行すると、3次元空間におけるリサージュ曲線が描画され、視覚的に楽しむことができます。

これらの応用例を通じて、リサージュ曲線の多様性と美しさを体験することができます。

まとめ

この記事では、Pythonのmatplotlibライブラリを使用してリサージュ曲線を描く方法について詳しく解説しました。

リサージュ曲線の基本的な概念から、具体的な描画手順、さらには応用例に至るまで、幅広く取り上げました。

リサージュ曲線の描画を通じて、データ可視化の楽しさや奥深さを体験し、さまざまなパラメータを調整することで異なる形状を生成することができるでしょう。

ぜひ、実際にコードを試してみて、リサージュ曲線の美しさを自分の手で描いてみてください。