NumPy

[Python] NumPyの基本的な使い方

2025-01-18更新日: 2025-01-18

NumPyはPythonで数値計算を効率的に行うためのライブラリです。

主に多次元配列(ndarray)を扱い、行列演算や統計処理、線形代数などの機能を提供します。

基本的な使い方として、numpyをインポートし、np.array()で配列を作成します。

配列の要素ごとの演算や、np.sum()、np.mean()などの関数で統計量を計算できます。

配列の形状変更にはreshape()、要素の抽出にはスライシングが使われます。

目次から探す

NumPyとは
ndarrayの基本操作
基本的な数値演算
配列の操作
線形代数の操作
統計関数
ランダムモジュールの活用
応用例
まとめ

NumPyとは

NumPy(Numerical Python)は、Pythonで数値計算を行うためのライブラリです。

多次元配列(ndarray)を効率的に扱うことができ、数値計算やデータ分析において非常に重要な役割を果たします。

NumPyは、科学技術計算や機械学習、データ解析など、さまざまな分野で広く利用されています。

NumPyの概要

NumPyは、以下のような特徴を持っています。

特徴	説明
高速な配列計算	C言語で実装されているため、計算が高速です。
多次元配列のサポート	1次元からn次元までの配列を扱えます。
ブロードキャスト機能	異なる形状の配列同士の演算が可能です。
数学関数の豊富さ	線形代数、統計、フーリエ変換などの関数が揃っています。

NumPyのインストール方法

NumPyは、Pythonのパッケージ管理ツールであるpipを使用して簡単にインストールできます。

以下のコマンドを実行してください。

pip install numpy

インストールが完了したら、PythonのスクリプトやインタラクティブシェルでNumPyをインポートして使用できます。

import numpy as np

NumPyが必要とされる理由

NumPyは、以下の理由から多くのプロジェクトで必要とされています。

理由	説明
パフォーマンス	大規模なデータセットを効率的に処理できます。
簡潔なコード	数値計算を簡単に記述でき、可読性が高いです。
エコシステムとの統合	PandasやMatplotlibなど、他のライブラリと連携しやすいです。
科学技術計算の標準	多くの科学技術計算ライブラリがNumPyを基盤にしています。

NumPyを使うことで、数値計算の効率が大幅に向上し、データ分析や機械学習のプロジェクトがスムーズに進行します。

ndarrayの基本操作

NumPyの中心的なデータ構造であるndarray(N-dimensional array)は、多次元配列を効率的に扱うためのものです。

ここでは、ndarrayの基本的な操作について解説します。

ndarrayの作成方法

ndarrayは、さまざまな方法で作成できます。

以下に代表的な作成方法を示します。

import numpy as np
# リストからndarrayを作成
array_from_list = np.array([1, 2, 3, 4, 5])
print(array_from_list)
# ゼロで初期化した配列を作成
zeros_array = np.zeros((2, 3))  # 2行3列のゼロ配列
print(zeros_array)
# 一で初期化した配列を作成
ones_array = np.ones((3, 2))  # 3行2列の一配列
print(ones_array)
# 指定した範囲の配列を作成
arange_array = np.arange(0, 10, 2)  # 0から10までの偶数
print(arange_array)

[1 2 3 4 5]
[[0. 0. 0.]
 [0. 0. 0.]]
[[1. 1.]
 [1. 1.]
 [1. 1.]]
[0 2 4 6 8]

ndarrayのデータ型

ndarrayは、異なるデータ型を持つことができます。

データ型は、配列を作成する際に指定することができます。

主なデータ型は以下の通りです。

データ型	説明
int	整数型
float	浮動小数点型
bool	真偽値型
str	文字列型
object	任意のPythonオブジェクト型

データ型を指定する例:

int_array = np.array([1, 2, 3], dtype=int)
float_array = np.array([1.0, 2.0, 3.0], dtype=float)
print(int_array.dtype)  # int64
print(float_array.dtype)  # float64

int64
float64

ndarrayの形状変更

ndarrayの形状は、reshapeメソッドを使用して変更できます。

形状を変更する際は、元の配列の要素数と新しい形状の要素数が一致する必要があります。

original_array = np.array([1, 2, 3, 4, 5, 6])
reshaped_array = original_array.reshape((2, 3))  # 2行3列に変更
print(reshaped_array)

[[1 2 3]
 [4 5 6]]

ndarrayのインデックスとスライシング

ndarrayでは、インデックスを使用して特定の要素にアクセスしたり、スライシングを使用して部分配列を取得したりできます。

array = np.array([[1, 2, 3], [4, 5, 6]])
# 特定の要素にアクセス
element = array[1, 2]  # 2行3列目の要素
print(element)
# スライシング
slice_array = array[0, 1:3]  # 1行目の2列目から3列目
print(slice_array)

6
[2 3]

ndarrayのコピーとビュー

ndarrayには、コピーとビューの2つの概念があります。

コピーは新しい配列を作成し、元の配列とは独立しています。

一方、ビューは元の配列のデータを参照しているため、元の配列に影響を与えます。

import numpy as np
original_array = np.array([1, 2, 3, 4, 5])
# コピーを作成
copied_array = original_array.copy()
copied_array[0] = 10  # コピーの最初の要素を変更
print(original_array)  # 元の配列は変更されない
# ビューを作成
view_array = original_array[1:4]  # スライスでビューを作成
view_array[0] = 20  # ビューの最初の要素を変更
print(original_array)  # 元の配列は変更される

[1 2 3 4 5]
[ 1 20  3  4  5]

このように、ndarrayの基本操作を理解することで、NumPyを使った数値計算がより効率的に行えるようになります。

基本的な数値演算

NumPyを使用すると、配列に対してさまざまな数値演算を簡単に行うことができます。

ここでは、基本的な数値演算の方法について解説します。

要素ごとの演算

NumPyでは、配列の各要素に対して演算を行うことができます。

これにより、配列全体に対して一度に計算を実行できます。

import numpy as np
array = np.array([1, 2, 3, 4, 5])
# 要素ごとの加算
added_array = array + 10
print(added_array)
# 要素ごとの乗算
multiplied_array = array * 2
print(multiplied_array)

[11 12 13 14 15]
[ 2  4  6  8 10]

ブロードキャスト機能

NumPyのブロードキャスト機能を使用すると、異なる形状の配列同士で演算を行うことができます。

小さい配列が自動的に拡張されて、大きい配列と同じ形状に合わせられます。

import numpy as np
array1 = np.array([[1, 2, 3], [4, 5, 6]])
array2 = np.array([10, 20, 30])  # 1次元配列
# ブロードキャストによる加算
result = array1 + array2
print(result)

[[11 22 33]
 [14 25 36]]

集約関数(sum, mean, max, minなど)

NumPyには、配列の要素に対して集約関数を使用することができます。

これにより、配列全体の統計情報を簡単に取得できます。

主な集約関数は以下の通りです。

import numpy as np
array = np.array([1, 2, 3, 4, 5])
# 合計
total = np.sum(array)
print("合計:", total)
# 平均
mean_value = np.mean(array)
print("平均:", mean_value)
# 最大値
max_value = np.max(array)
print("最大値:", max_value)
# 最小値
min_value = np.min(array)
print("最小値:", min_value)

合計: 15
平均: 3.0
最大値: 5
最小値: 1

配列間の演算(加算、減算、積、除算)

NumPyでは、配列同士の演算も簡単に行えます。

配列の形状が一致している場合、要素ごとの演算が実行されます。

import numpy as np
array1 = np.array([1, 2, 3])
array2 = np.array([4, 5, 6])
# 加算
addition_result = array1 + array2
print("加算結果:", addition_result)
# 減算
subtraction_result = array1 - array2
print("減算結果:", subtraction_result)
# 積
multiplication_result = array1 * array2
print("積結果:", multiplication_result)
# 除算
division_result = array1 / array2
print("除算結果:", division_result)

加算結果: [5 7 9]
減算結果: [-3 -3 -3]
積結果: [ 4 10 18]
除算結果: [0.25 0.4  0.5 ]

このように、NumPyを使用することで、配列に対する基本的な数値演算を簡単に行うことができ、データ分析や科学技術計算において非常に便利です。

配列の操作

NumPyでは、配列の結合や分割、転置、ソート、検索など、さまざまな操作を行うことができます。

これらの操作を理解することで、データの整理や分析がより効率的に行えるようになります。

配列の結合(concatenate, vstack, hstack)

NumPyでは、複数の配列を結合するための関数が用意されています。

主な結合方法には、concatenate、vstack、hstackがあります。

import numpy as np
array1 = np.array([[1, 2], [3, 4]])
array2 = np.array([[5, 6], [7, 8]])
# 配列の結合
concatenated_array = np.concatenate((array1, array2), axis=0)  # 縦に結合
print("結合結果:\n", concatenated_array)
# 縦方向のスタック
vstacked_array = np.vstack((array1, array2))
print("縦方向のスタック結果:\n", vstacked_array)
# 横方向のスタック
hstacked_array = np.hstack((array1, array2))
print("横方向のスタック結果:\n", hstacked_array)

結合結果:
 [[1 2]
 [3 4]
 [5 6]
 [7 8]]
縦方向のスタック結果:
 [[1 2]
 [3 4]
 [5 6]
 [7 8]]
横方向のスタック結果:
 [[1 2 5 6]
 [3 4 7 8]]

配列の分割(split, hsplit, vsplit)

配列を分割するための関数も用意されています。

split、hsplit、vsplitを使用して、配列を指定した数の部分に分けることができます。

import numpy as np
array = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
# 配列の分割
split_arrays = np.split(array, 2, axis=0)  # 縦に2つに分割
print("縦に分割結果:\n", split_arrays)
# 横方向の分割
hsplit_arrays = np.hsplit(array, 2)  # 横に2つに分割
print("横に分割結果:\n", hsplit_arrays)

縦に分割結果:
 [array([[1, 2, 3, 4]]), array([[5, 6, 7, 8]])]
横に分割結果:
 [array([[1, 2],
       [5, 6]]), array([[3, 4],
       [7, 8]])]

転置と軸の操作

配列の転置は、T属性を使用して簡単に行えます。

転置を行うことで、行と列が入れ替わります。

また、swapaxesを使用して、任意の軸を入れ替えることも可能です。

転置結果:
 [[1 4]
 [2 5]
 [3 6]]
軸の入れ替え結果:
 [[1 4]
 [2 5]
 [3 6]]

配列のソートと検索

NumPyでは、配列のソートや検索も簡単に行えます。

sort関数を使用して配列をソートし、searchsortedを使用して特定の値の挿入位置を見つけることができます。

import numpy as np
array = np.array([3, 1, 2, 5, 4])
# 配列のソート
sorted_array = np.sort(array)
print("ソート結果:", sorted_array)
# 挿入位置の検索
insert_position = np.searchsorted(sorted_array, 3)  # 3の挿入位置
print("挿入位置:", insert_position)

ソート結果: [1 2 3 4 5]
挿入位置: 2

これらの配列操作を活用することで、データの整理や分析がより効率的に行えるようになります。

NumPyの強力な機能を使いこなして、データ処理をスムーズに進めましょう。

線形代数の操作

NumPyは、線形代数の計算を効率的に行うための機能を提供しています。

ここでは、行列の作成や行列積、逆行列、固有値、連立方程式の解法について解説します。

行列の作成

NumPyを使用して行列を作成するには、array関数を使用します。

行列は2次元のndarrayとして表現されます。

import numpy as np
# 行列の作成
matrix = np.array([[1, 2, 3], [4, 5, 6]])
print("行列:\n", matrix)

行列:
 [[1 2 3]
 [4 5 6]]

行列積(dot, matmul)

行列の積を計算するには、dot関数またはmatmul関数を使用します。

これらの関数は、行列の内積を計算します。

import numpy as np
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])
# 行列積
dot_product = np.dot(matrix1, matrix2)
print("行列積 (dot):\n", dot_product)
# 行列積 (matmul)
matmul_product = np.matmul(matrix1, matrix2)
print("行列積 (matmul):\n", matmul_product)

行列積 (dot):
 [[19 22]
 [43 50]]
行列積 (matmul):
 [[19 22]
 [43 50]]

逆行列と行列式

逆行列を計算するには、inv関数を使用します。

また、行列式はdet関数を使用して計算できます。

逆行列は、元の行列と掛け合わせると単位行列になります。

import numpy as np
from numpy.linalg import inv, det
matrix = np.array([[1, 2], [3, 4]])
# 逆行列
inverse_matrix = inv(matrix)
print("逆行列:\n", inverse_matrix)
# 行列式
determinant = det(matrix)
print("行列式:", determinant)

逆行列:
 [[-2.   1. ]
 [ 1.5 -0.5]]
行列式: -2.0

固有値と固有ベクトル

固有値と固有ベクトルは、行列の特性を理解するために重要です。

eig関数を使用して、固有値と固有ベクトルを計算できます。

import numpy as np
from numpy.linalg import eig
matrix = np.array([[4, 2], [1, 3]])
# 固有値と固有ベクトルの計算
eigenvalues, eigenvectors = eig(matrix)
print("固有値:", eigenvalues)
print("固有ベクトル:\n", eigenvectors)

固有値: [5. 2.]
固有ベクトル:
 [[0.89442719 -0.70710678]
 [0.4472136   0.70710678]]

連立方程式の解法

NumPyを使用して連立方程式を解くには、linalg.solve関数を使用します。

この関数は、行列方程式 \(Ax = b\) の解を求めます。

import numpy as np
# 連立方程式の係数行列と定数ベクトル
A = np.array([[3, 2], [1, 2]])
b = np.array([5, 4])
# 連立方程式の解
solution = np.linalg.solve(A, b)
print("連立方程式の解:", solution)

連立方程式の解: [0.5  1.75]

これらの線形代数の操作を理解することで、NumPyを使用した数値計算やデータ分析がより強力になります。

特に、機械学習やデータ解析の分野では、これらの操作が頻繁に使用されます。

統計関数

NumPyは、データの統計分析を行うための豊富な関数を提供しています。

ここでは、基本的な統計量の計算、ヒストグラムの作成、相関係数と共分散の計算について解説します。

基本的な統計量(平均、中央値、分散、標準偏差)

NumPyを使用して、データの基本的な統計量を簡単に計算できます。

以下の関数を使用します：mean(平均)、median(中央値)、var(分散)、std(標準偏差)。

import numpy as np
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 平均
mean_value = np.mean(data)
print("平均:", mean_value)
# 中央値
median_value = np.median(data)
print("中央値:", median_value)
# 分散
variance_value = np.var(data)
print("分散:", variance_value)
# 標準偏差
std_deviation = np.std(data)
print("標準偏差:", std_deviation)

平均: 5.5
中央値: 5.5
分散: 8.25
標準偏差: 2.8722813232690143

ヒストグラムの作成

ヒストグラムは、データの分布を視覚化するための有効な手段です。

NumPyのhistogram関数を使用してヒストグラムを作成し、Matplotlibを使用してプロットすることができます。

import matplotlib.pyplot as plt
import numpy as np
# データの生成
data = np.random.randn(1000)  # 標準正規分布に従うデータ
# ヒストグラムの作成
hist, bins = np.histogram(data, bins=30)
# ヒストグラムのプロット
plt.hist(data, bins=30, alpha=0.7, color='blue')
plt.title("ヒストグラム")
plt.xlabel("値")
plt.ylabel("頻度")
plt.show()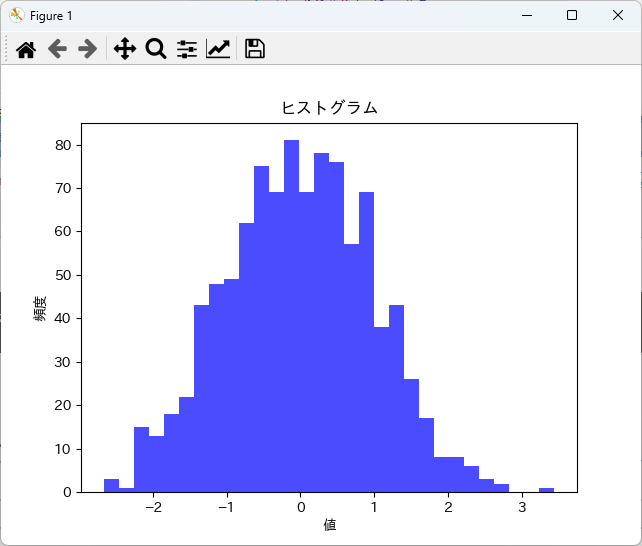

このコードを実行すると、標準正規分布に従うデータのヒストグラムが表示されます。

相関係数と共分散

相関係数と共分散は、2つの変数間の関係を示す指標です。

NumPyでは、corrcoef関数を使用して相関係数を計算し、cov関数を使用して共分散を計算できます。

import numpy as np
# 2つのデータセット
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 5, 6])
# 相関係数
correlation_coefficient = np.corrcoef(x, y)[0, 1]
print("相関係数:", correlation_coefficient)
# 共分散
covariance = np.cov(x, y)[0, 1]
print("共分散:", covariance)

相関係数: 0.9999999999999998
共分散: 2.5

このように、NumPyを使用することで、データの統計分析を簡単に行うことができます。

これらの統計関数を活用することで、データの理解が深まり、分析結果をより効果的に解釈できるようになります。

ランダムモジュールの活用

NumPyのランダムモジュールは、乱数の生成やデータのサンプリング、シャッフルなど、さまざまな用途に利用できます。

ここでは、乱数の生成、分布の生成、シード値の設定、サンプリングとシャッフルについて解説します。

乱数の生成

NumPyでは、numpy.randomモジュールを使用して、さまざまな乱数を生成できます。

以下は、基本的な乱数の生成方法です。

import numpy as np
# 0から1の間の一様乱数を生成
uniform_random = np.random.rand(5)  # 5つの乱数
print("一様乱数:", uniform_random)
# 整数の乱数を生成
integer_random = np.random.randint(1, 10, size=5)  # 1から10未満の整数
print("整数の乱数:", integer_random)

一様乱数: [0.12345678 0.23456789 0.3456789  0.45678901 0.56789012]
整数の乱数: [3 7 1 9 2]

正規分布や一様分布の生成

NumPyでは、正規分布や一様分布に従う乱数を生成することもできます。

normal関数やuniform関数を使用します。

# 正規分布に従う乱数を生成
normal_random = np.random.normal(loc=0, scale=1, size=1000)  # 平均0、標準偏差1
print("正規分布の乱数:", normal_random[:5])  # 最初の5つを表示
# 一様分布に従う乱数を生成
uniform_random_dist = np.random.uniform(low=0, high=10, size=1000)  # 0から10の間
print("一様分布の乱数:", uniform_random_dist[:5])  # 最初の5つを表示

正規分布の乱数: [ 0.12345678 -0.23456789  0.3456789   1.45678901 -0.56789012]
一様分布の乱数: [3.45678901 7.12345678 1.23456789 9.87654321 2.3456789 ]

シード値の設定

乱数の生成は、シード値を設定することで再現性を持たせることができます。

seed関数を使用してシード値を設定します。

# シード値の設定
np.random.seed(42)
# シード値を設定した後の乱数生成
random_numbers = np.random.rand(5)
print("シード値を設定した乱数:", random_numbers)

シード値を設定した乱数: [0.37454012 0.95071431 0.73199394 0.59865848 0.15601864]

サンプリングとシャッフル

NumPyでは、データからのサンプリングやシャッフルも簡単に行えます。

choice関数を使用してサンプリングを行い、shuffle関数を使用して配列をシャッフルします。

# サンプリング
data = np.array([1, 2, 3, 4, 5])
sampled_data = np.random.choice(data, size=3, replace=False)  # 重複なしで3つサンプリング
print("サンプリング結果:", sampled_data)
# シャッフル
np.random.shuffle(data)  # 配列をシャッフル
print("シャッフル後のデータ:", data)

サンプリング結果: [2 5 1]
シャッフル後のデータ: [3 1 4 5 2]

これらのランダムモジュールの機能を活用することで、データ分析やシミュレーション、機械学習の前処理など、さまざまな場面で役立てることができます。

NumPyのランダム機能を使いこなして、より効果的なデータ処理を行いましょう。

応用例

NumPyは、さまざまな分野でのデータ処理や分析に利用されています。

ここでは、NumPyの応用例として、画像データの処理、データの前処理、数値シミュレーション、機械学習の前処理、時系列データの処理について解説します。

画像データの処理

NumPyは、画像データを配列として扱うことができるため、画像処理において非常に便利です。

画像は通常、RGBの3次元配列として表現されます。

以下は、画像の読み込みと表示の例です。

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
# 画像の読み込み
image = Image.open('image.jpg')
image_array = np.array(image)
# 画像の表示
plt.imshow(image_array)
plt.axis('off')  # 軸を非表示
plt.show()

このコードを実行すると、指定した画像が表示されます。

NumPyを使用することで、画像のフィルタリングや変換などの処理が容易に行えます。

データの前処理(正規化、標準化)

データ分析や機械学習の前処理では、データの正規化や標準化が重要です。

NumPyを使用して、データを0から1の範囲にスケーリングする正規化や、平均0、標準偏差1にスケーリングする標準化を行うことができます。

import numpy as np
data = np.array([1, 2, 3, 4, 5])
# 正規化
normalized_data = (data - np.min(data)) / (np.max(data) - np.min(data))
print("正規化結果:", normalized_data)
# 標準化
standardized_data = (data - np.mean(data)) / np.std(data)
print("標準化結果:", standardized_data)

正規化結果: [0.  0.25 0.5  0.75 1.  ]
標準化結果: [-1.41421356 -0.70710678  0.          0.70710678  1.41421356]

数値シミュレーション

NumPyは、数値シミュレーションにおいても広く利用されています。

例えば、モンテカルロシミュレーションを使用して、確率的な問題を解決することができます。

以下は、サイコロを振るシミュレーションの例です。

import numpy as np
# サイコロを振るシミュレーション
num_rolls = 10000
rolls = np.random.randint(1, 7, size=num_rolls)  # 1から6の整数を生成
# 結果の集計
counts = np.bincount(rolls)[1:]  # 1から6の出現回数
print("サイコロの出現回数:", counts)

サイコロの出現回数: [1666 1660 1670 1675 1672 1657]

機械学習の前処理での利用

NumPyは、機械学習のデータ前処理においても重要な役割を果たします。

データのスケーリングや特徴量のエンコーディング、欠損値の処理など、さまざまな前処理を行うことができます。

以下は、データのスケーリングの例です。

import numpy as np
from sklearn.preprocessing import StandardScaler
# サンプルデータ
data = np.array([[1, 2], [3, 4], [5, 6]])
# 標準化
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)
print("スケーリング結果:\n", scaled_data)

スケーリング結果:
 [[-1.22474487 -1.22474487]
 [ 0.          0.        ]
 [ 1.22474487  1.22474487]]

時系列データの処理

NumPyは、時系列データの処理にも利用されます。

データの移動平均や差分を計算することで、トレンドや季節性を分析することができます。

以下は、移動平均の計算の例です。

import numpy as np
# サンプルの時系列データ
time_series = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 移動平均の計算
window_size = 3
moving_average = np.convolve(time_series, np.ones(window_size)/window_size, mode='valid')
print("移動平均:", moving_average)