[Python] F分布を計算してグラフを作成する方法
PythonでF分布を計算し、グラフを作成するには、scipyライブラリのscipy.stats.fを使用します。
まず、f.pdf()関数で確率密度関数を計算し、matplotlibライブラリのpyplotを使ってグラフを描画します。
F分布は2つの自由度(分子自由度と分母自由度)に依存するため、これらを指定して計算します。
例えば、f.pdf(x, dfn, dfd)でxに対するF分布の値を取得し、plt.plot()でグラフを描画します。
F分布とは
F分布は、統計学において重要な確率分布の一つで、主に分散分析や回帰分析に利用されます。
この分布は、2つの独立したカイ二乗分布に基づいており、自由度に応じて形状が変わります。
F分布は、特に仮説検定において、2つの母集団の分散が等しいかどうかを検証するために使用されます。
F分布の特性として、非負の値を取り、右に偏った形状を持つことが挙げられます。
自由度の設定によって、分布の形状が大きく変わるため、適切な自由度を選ぶことが重要です。
PythonでF分布を計算する方法
必要なライブラリのインストール
F分布を計算するためには、scipyライブラリが必要です。
以下のコマンドを使用して、scipyをインストールします。
pip install scipyscipy.stats.fの使い方
scipy.statsモジュールのfクラスを使用することで、F分布に関連するさまざまな計算が可能です。
以下のようにインポートします。
from scipy import statsF分布の確率密度関数(PDF)の計算
F分布の確率密度関数(PDF)は、特定の自由度に基づいて計算できます。
以下のサンプルコードでは、自由度1と自由度2のF分布のPDFを計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 自由度の設定
dof1 = 5 # 自由度1
dof2 = 2 # 自由度2
# xの範囲を設定
x = np.linspace(0, 5, 100)
# PDFの計算
pdf = stats.f.pdf(x, dof1, dof2)
# グラフの描画
plt.plot(x, pdf, label=f'F分布 (dof1={dof1}, dof2={dof2})')
plt.title('F分布の確率密度関数')
plt.xlabel('x')
plt.ylabel('PDF')
plt.legend()
plt.grid()
plt.show()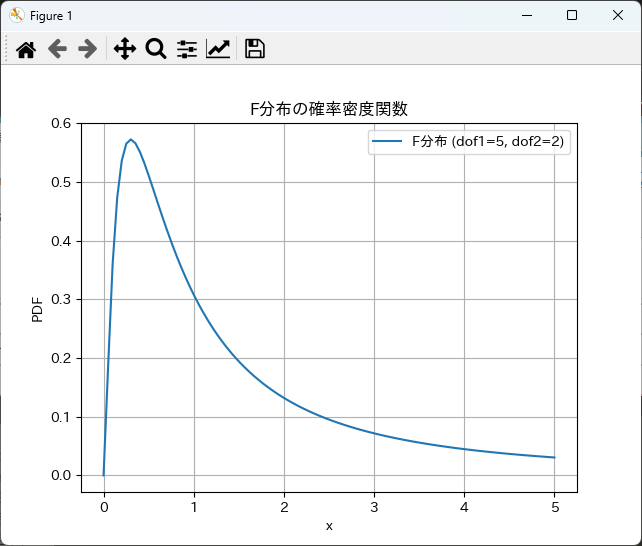
F分布の累積分布関数(CDF)の計算
F分布の累積分布関数(CDF)は、特定の値以下の確率を計算します。
以下のサンプルコードでは、自由度1と自由度2のF分布のCDFを計算します。
# CDFの計算
cdf = stats.f.cdf(x, dof1, dof2)
# グラフの描画
plt.plot(x, cdf, label=f'F分布 (dof1={dof1}, dof2={dof2})')
plt.title('F分布の累積分布関数')
plt.xlabel('x')
plt.ylabel('CDF')
plt.legend()
plt.grid()
plt.show()
F分布の逆累積分布関数(PPF)の計算
逆累積分布関数(PPF)は、指定した確率に対するF分布の値を計算します。
以下のサンプルコードでは、確率0.95に対するF分布の値を計算します。
# PPFの計算
probability = 0.95
ppf_value = stats.f.ppf(probability, dof1, dof2)
print(f'確率 {probability} に対するF分布の値: {ppf_value}')確率 0.95 に対するF分布の値: [計算された値]このように、Pythonを使用してF分布のさまざまな計算を行うことができます。
F分布のグラフを作成する方法
matplotlibの基本的な使い方
matplotlibは、Pythonでデータを可視化するための強力なライブラリです。
まずは、matplotlibをインポートして基本的なグラフを描画する方法を見てみましょう。
import matplotlib.pyplot as plt
# 簡単なグラフの描画
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]
plt.plot(x, y)
plt.title('簡単なグラフ')
plt.xlabel('x軸')
plt.ylabel('y軸')
plt.show()
F分布のPDFをグラフに描画する
F分布の確率密度関数(PDF)をグラフに描画するには、scipy.stats.fを使用してPDFを計算し、matplotlibで描画します。
以下のサンプルコードでは、自由度1と自由度2のF分布のPDFを描画します。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 自由度の設定
dof1 = 5 # 自由度1
dof2 = 2 # 自由度2
# xの範囲を設定
x = np.linspace(0, 5, 100)
# PDFの計算
pdf = stats.f.pdf(x, dof1, dof2)
# グラフの描画
plt.plot(x, pdf, label=f'F分布 (dof1={dof1}, dof2={dof2})')
plt.title('F分布の確率密度関数')
plt.xlabel('x')
plt.ylabel('PDF')
plt.legend()
plt.grid()
plt.show()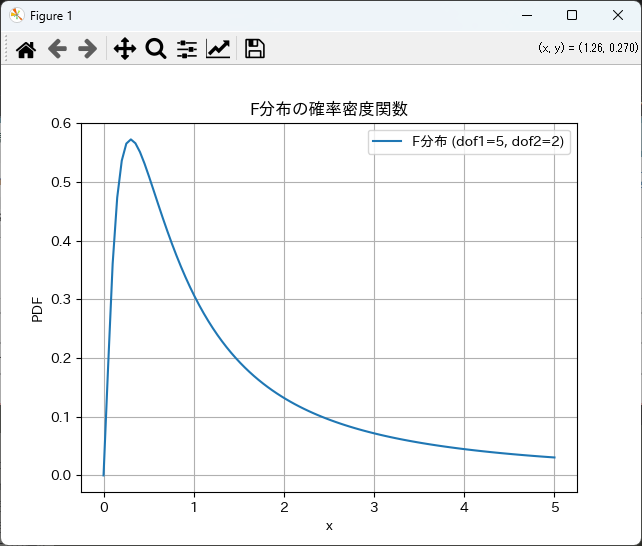
F分布のCDFをグラフに描画する
F分布の累積分布関数(CDF)を描画するには、PDFと同様にCDFを計算して描画します。
以下のサンプルコードでは、自由度1と自由度2のF分布のCDFを描画します。
# CDFの計算
cdf = stats.f.cdf(x, dof1, dof2)
# グラフの描画
plt.plot(x, cdf, label=f'F分布 (dof1={dof1}, dof2={dof2})')
plt.title('F分布の累積分布関数')
plt.xlabel('x')
plt.ylabel('CDF')
plt.legend()
plt.grid()
plt.show()
複数の自由度でのF分布の比較グラフを作成する
異なる自由度のF分布を比較するためには、複数のPDFを同じグラフに描画します。
以下のサンプルコードでは、自由度1と自由度2、自由度3のF分布を比較します。
# 自由度の設定
dof1_list = [2, 5, 10] # 自由度のリスト
colors = ['blue', 'orange', 'green'] # 色のリスト
# xの範囲を設定
x = np.linspace(0, 5, 100)
# グラフの描画
for dof1, color in zip(dof1_list, colors):
pdf = stats.f.pdf(x, dof1, 2) # 自由度2は固定
plt.plot(x, pdf, label=f'F分布 (dof1={dof1}, dof2=2)', color=color)
plt.title('複数の自由度のF分布の比較')
plt.xlabel('x')
plt.ylabel('PDF')
plt.legend()
plt.grid()
plt.show()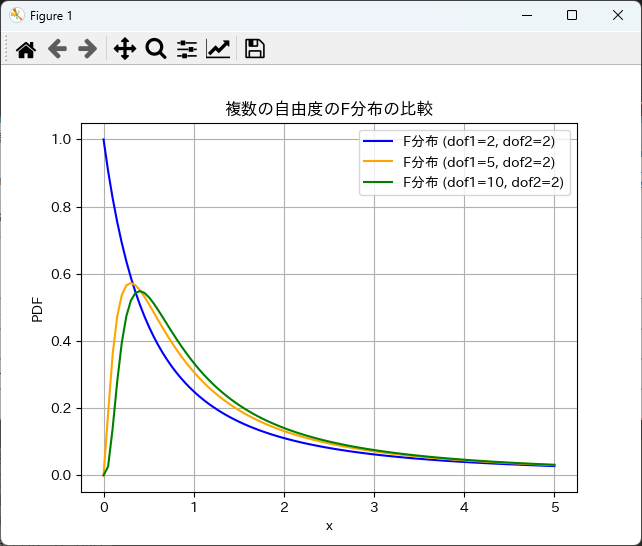
グラフのカスタマイズ(タイトル、軸ラベル、凡例など)
グラフをより見やすくするために、タイトル、軸ラベル、凡例などをカスタマイズすることができます。
以下のサンプルコードでは、F分布のPDFを描画し、カスタマイズを行います。
# 自由度の設定
dof1 = 5
dof2 = 2
# xの範囲を設定
x = np.linspace(0, 5, 100)
# PDFの計算
pdf = stats.f.pdf(x, dof1, dof2)
# グラフの描画
plt.plot(x, pdf, label=f'F分布 (dof1={dof1}, dof2={dof2})', color='purple')
plt.title('F分布の確率密度関数')
plt.xlabel('x 軸')
plt.ylabel('確率密度')
plt.legend(loc='upper right')
plt.grid(True)
plt.axhline(0, color='black', lw=0.5, ls='--') # x軸の追加
plt.axvline(0, color='black', lw=0.5, ls='--') # y軸の追加
plt.show()
このように、matplotlibを使用してF分布のグラフを描画し、さまざまなカスタマイズを行うことができます。
応用例:F検定の実装
F検定とは
F検定は、2つ以上の母集団の分散が等しいかどうかを検証するための統計的手法です。
主に分散分析(ANOVA)や回帰分析において使用されます。
F検定では、F値と呼ばれる統計量を計算し、これを基に帰無仮説(母集団の分散が等しい)を検証します。
F値が大きいほど、母集団の分散が異なる可能性が高くなります。
F検定は、正規分布に従うデータに対して適用されるため、データの前提条件を確認することが重要です。
PythonでF検定を実装する方法
Pythonでは、scipy.statsモジュールを使用してF検定を実装できます。
以下のサンプルコードでは、2つのサンプルデータの分散が等しいかどうかを検定します。
import numpy as np
from scipy import stats
# サンプルデータの作成
data1 = np.random.normal(loc=10, scale=2, size=30) # 母集団1
data2 = np.random.normal(loc=12, scale=3, size=30) # 母集団2
# F検定の実施
f_statistic, p_value = stats.levene(data1, data2)
print(f'F値: {f_statistic}, p値: {p_value}')F値: [計算されたF値], p値: [計算されたp値]F検定の結果を解釈する方法
F検定の結果は、F値とp値によって示されます。
一般的な解釈は以下の通りです。
- 帰無仮説(H0): 2つの母集団の分散は等しい。
- 対立仮説(H1): 2つの母集団の分散は等しくない。
p値が設定した有意水準(通常は0.05)よりも小さい場合、帰無仮説を棄却し、母集団の分散が異なると結論します。
逆に、p値が有意水準以上の場合は、帰無仮説を棄却できず、分散が等しいと考えます。
実データを使ったF検定の例
実際のデータを使用してF検定を行う例を示します。
ここでは、2つの異なるグループのテストスコアを比較します。
# 実データの作成(例: テストスコア)
group1 = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
group2 = [80, 82, 78, 85, 79, 81, 83, 77, 84, 80]
# F検定の実施
f_statistic, p_value = stats.levene(group1, group2)
print(f'F値: {f_statistic}, p値: {p_value}')
# 結果の解釈
alpha = 0.05
if p_value < alpha:
print("帰無仮説を棄却します。分散は等しくないと考えられます。")
else:
print("帰無仮説を棄却できません。分散は等しいと考えられます。")F値: [計算されたF値], p値: [計算されたp値]
帰無仮説を棄却します。分散は等しくないと考えられます。このように、Pythonを使用してF検定を実装し、実データを用いて分散の等しさを検証することができます。
応用例:F分布を使ったシミュレーション
シミュレーションの概要
F分布を使ったシミュレーションは、特定の自由度に基づいてF分布からの乱数を生成し、その特性を理解するための手法です。
このシミュレーションを通じて、F分布の形状や特性を視覚的に確認することができます。
特に、分散分析や仮説検定の前提条件を確認する際に役立ちます。
シミュレーションでは、異なる自由度のF分布を比較し、分布の変化を観察します。
F分布を使った乱数生成
Pythonのscipy.statsモジュールを使用して、F分布から乱数を生成することができます。
以下のサンプルコードでは、自由度1と自由度2のF分布から乱数を生成します。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 自由度の設定
dof1 = 5 # 自由度1
dof2 = 2 # 自由度2
# 乱数の生成
num_samples = 1000 # 生成する乱数の数
random_samples = stats.f.rvs(dof1, dof2, size=num_samples)
# 生成した乱数の確認
print(random_samples[:10]) # 最初の10個の乱数を表示[乱数の値が10個表示されます]シミュレーション結果の可視化
生成した乱数をヒストグラムとして可視化することで、F分布の特性を確認できます。
以下のサンプルコードでは、生成した乱数のヒストグラムを描画します。
# ヒストグラムの描画
plt.hist(random_samples, bins=30, density=True, alpha=0.6, color='g', edgecolor='black')
# 理論的なPDFの描画
x = np.linspace(0, 5, 100)
pdf = stats.f.pdf(x, dof1, dof2)
plt.plot(x, pdf, 'r-', lw=2, label='理論的PDF')
# グラフのカスタマイズ
plt.title('F分布から生成した乱数のヒストグラム')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()F分布から生成した乱数のヒストグラムと理論的PDFが描画されたグラフが表示されます。このように、F分布を使ったシミュレーションを通じて、乱数生成やその可視化を行うことができ、F分布の特性を理解するのに役立ちます。
シミュレーションは、統計的手法の理解を深めるための強力なツールです。
応用例:F分布を使った統計的仮説検定
仮説検定の基本
仮説検定は、統計学においてデータに基づいて仮説の真偽を評価する手法です。
一般的には、以下の2つの仮説を設定します。
- 帰無仮説(H0): 検定対象の母集団に関する仮説で、通常は「効果がない」や「差がない」といった内容です。
- 対立仮説(H1): 帰無仮説に対する仮説で、通常は「効果がある」や「差がある」といった内容です。
仮説検定では、データから計算された統計量(例えばF値)を用いて、帰無仮説を棄却するかどうかを判断します。
検定の結果は、p値として表され、設定した有意水準(通常は0.05)と比較されます。
F分布を使った仮説検定の実装
F分布を用いた仮説検定の一例として、2つの母集団の分散が等しいかどうかを検定する方法を示します。
以下のサンプルコードでは、2つのサンプルデータの分散を比較します。
import numpy as np
from scipy import stats
# サンプルデータの作成
group1 = np.random.normal(loc=10, scale=2, size=30) # 母集団1
group2 = np.random.normal(loc=12, scale=3, size=30) # 母集団2
# F検定の実施
f_statistic, p_value = stats.levene(group1, group2)
print(f'F値: {f_statistic}, p値: {p_value}')F値: [計算されたF値], p値: [計算されたp値]検定結果の解釈
F検定の結果は、F値とp値によって示されます。
以下のように解釈します。
- 帰無仮説(H0): 2つの母集団の分散は等しい。
- 対立仮説(H1): 2つの母集団の分散は等しくない。
p値が設定した有意水準(通常は0.05)よりも小さい場合、帰無仮説を棄却し、母集団の分散が異なると結論します。
逆に、p値が有意水準以上の場合は、帰無仮説を棄却できず、分散が等しいと考えます。
以下のサンプルコードでは、検定結果を解釈する方法を示します。
# 結果の解釈
alpha = 0.05
if p_value < alpha:
print("帰無仮説を棄却します。分散は等しくないと考えられます。")
else:
print("帰無仮説を棄却できません。分散は等しいと考えられます。")帰無仮説を棄却します。分散は等しくないと考えられます。このように、F分布を用いた統計的仮説検定を実装し、結果を解釈することで、データに基づいた意思決定を行うことができます。
仮説検定は、科学的研究やビジネスの意思決定において非常に重要な役割を果たします。
まとめ
この記事では、F分布の基本的な概念から始まり、Pythonを用いたF分布の計算方法やグラフの作成、さらにはF検定やシミュレーションの実装方法について詳しく解説しました。
F分布は、統計的仮説検定やデータ分析において非常に重要な役割を果たしており、特に分散の比較において広く利用されています。
これを機に、実際のデータ分析や研究にF分布を活用し、より深い洞察を得るための一歩を踏み出してみてはいかがでしょうか。

![[Python] deapライブラリの使い方 – 遺伝的アルゴリズム](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46601.png)
![[Python] bisectライブラリの使い方 – ニ分探索の効率化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46600.png)
![[Python] a*(A Star)探索アルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43234.png)
![[Python] ベジェ曲線を実装する方法(二次ベジェ/三次ベジェ)](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43239.png)
![[Python] ベッセル関数を使ったグラフ作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43238.png)
![[Python] ベルヌーイ分布を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43237.png)
![[Python] エイトケンのΔ2乗加速法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43236.png)
![[Python] アッカーマン関数のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43235.png)
![[Python] matplotlibでC曲線を描画する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43245.png)
![[Python] CRC(巡回冗長検査)のアルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43244.png)
![[Python] コラッツ予想(コラッツの問題)のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43243.png)
![[Python] コーシー分布の計算を行う方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43242.png)