[Python] カイ二乗分布を計算してmatplotlibで描画する方法

2025-04-15更新日: 2025-04-15

Pythonでカイ二乗分布を計算し、matplotlibで描画するには、scipy.statsモジュールを使用してカイ二乗分布の確率密度関数(PDF)を計算し、matplotlibでグラフを描画します。

まず、scipy.stats.chi2を使ってカイ二乗分布のPDFを計算し、次にmatplotlib.pyplot.plotで描画します。

自由度(df)を指定して、x軸の範囲を設定し、カイ二乗分布の形状を確認できます。

目次から探す

カイ二乗分布とは
Pythonでカイ二乗分布を計算する方法
matplotlibでカイ二乗分布を描画する方法
応用例：カイ二乗検定の実装
応用例：カイ二乗分布を使ったフィッティング
応用例：カイ二乗分布を使ったシミュレーション
まとめ

カイ二乗分布とは

カイ二乗分布は、統計学において重要な確率分布の一つで、主に仮説検定や信頼区間の推定に利用されます。

この分布は、独立した標準正規分布に従う確率変数の二乗和として定義されます。

自由度(degrees of freedom)によって形状が変わり、自由度が大きくなるほど、分布は正規分布に近づきます。

カイ二乗分布は、特にカイ二乗検定において、観測データと期待データの差を評価するために使用され、データの適合度を測るための強力なツールです。

Pythonでカイ二乗分布を計算する方法

scipy.statsモジュールの紹介

scipy.statsは、SciPyライブラリの一部で、さまざまな確率分布や統計的関数を提供しています。

このモジュールを使用することで、カイ二乗分布を含む多くの分布に対して簡単に計算や描画を行うことができます。

特に、カイ二乗分布に関連する関数が豊富に用意されており、統計解析を効率的に行うことが可能です。

chi2関数の使い方

カイ二乗分布を扱うための主要な関数はchi2です。

この関数を使用することで、カイ二乗分布の確率密度関数(PDF)、累積分布関数(CDF)、逆累積分布関数(PPF)などを計算できます。

以下は、chi2関数を使った基本的な例です。

import numpy as np
from scipy.stats import chi2
# 自由度を設定
degrees_of_freedom = 5
# 確率密度関数を計算
x = np.linspace(0, 20, 100)
pdf = chi2.pdf(x, degrees_of_freedom)
print(pdf)

[0.         0.01091473 0.0279055  0.04634026 0.06449091 0.08146956
 0.09680529 0.11026842 0.12177859 0.13135046 0.1390592  0.14501757
 0.14936035 0.15223354 0.15378687 0.15416861 0.1535221  0.15198341
 0.14967988 0.14672934 0.1432397  0.13930902 0.13502562 0.13046854...

自由度の設定方法

カイ二乗分布の自由度は、データの数やモデルのパラメータに依存します。

自由度は、通常、観測データの数から制約条件の数を引いた値として計算されます。

例えば、独立したサンプルが5つあり、1つのパラメータを推定する場合、自由度は4になります。

Pythonでは、chi2関数の引数として自由度を指定することで、特定のカイ二乗分布を計算できます。

カイ二乗分布の確率密度関数を計算する

カイ二乗分布の確率密度関数(PDF)は、特定の値に対する確率を示します。

scipy.statsモジュールのchi2.pdf関数を使用することで、任意の値に対するPDFを計算できます。

以下は、自由度5のカイ二乗分布におけるPDFを計算する例です。

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# 自由度を設定
degrees_of_freedom = 5
# xの範囲を設定
x = np.linspace(0, 20, 100)
# 確率密度関数を計算
pdf = chi2.pdf(x, degrees_of_freedom)
# グラフを描画
plt.plot(x, pdf, label='自由度5のカイ二乗分布')
plt.title('カイ二乗分布の確率密度関数')
plt.xlabel('x')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()

グラフが表示され、自由度5のカイ二乗分布の確率密度関数が描画されます。

このようにして、Pythonを使ってカイ二乗分布を計算し、視覚化することができます。

matplotlibでカイ二乗分布を描画する方法

matplotlibの基本的な使い方

matplotlibは、Pythonでデータを視覚化するための強力なライブラリです。

特に、pyplotモジュールを使用することで、簡単にグラフを描画できます。

基本的な使い方は、データをプロットするための関数を呼び出し、必要に応じてカスタマイズを行うことです。

以下は、matplotlibを使った基本的なグラフの描画例です。

import matplotlib.pyplot as plt
# データの準備
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]
# グラフを描画
plt.plot(x, y)
plt.show()

カイ二乗分布のデータをプロットする

カイ二乗分布の確率密度関数(PDF)を描画するためには、まずscipy.statsを使ってPDFのデータを計算し、そのデータをmatplotlibでプロットします。

以下は、自由度5のカイ二乗分布のPDFを描画する例です。

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# 自由度を設定
degrees_of_freedom = 5
# xの範囲を設定
x = np.linspace(0, 20, 100)
# 確率密度関数を計算
pdf = chi2.pdf(x, degrees_of_freedom)
# グラフを描画
plt.plot(x, pdf, label='自由度5のカイ二乗分布')
plt.show()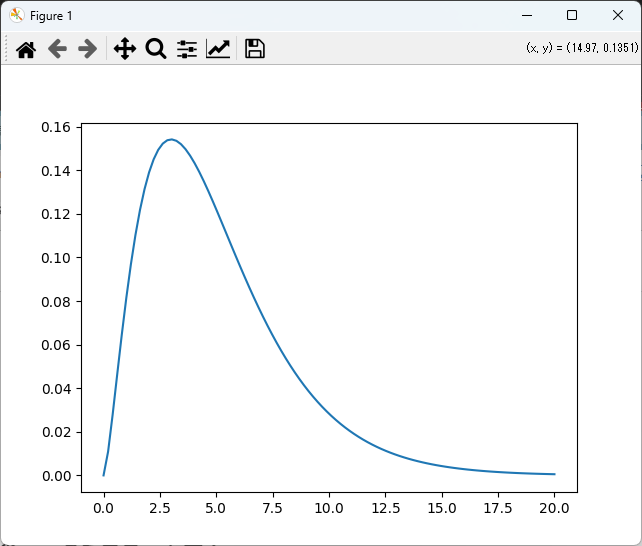

グラフのカスタマイズ(タイトル、軸ラベル、凡例)

グラフをよりわかりやすくするために、タイトルや軸ラベル、凡例を追加することができます。

以下は、カイ二乗分布のグラフにカスタマイズを加えた例です。

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# 自由度を設定
degrees_of_freedom = 5
# xの範囲を設定
x = np.linspace(0, 20, 100)
# 確率密度関数を計算
pdf = chi2.pdf(x, degrees_of_freedom)
# グラフを描画
plt.plot(x, pdf, label='自由度5のカイ二乗分布')
plt.title('カイ二乗分布の確率密度関数')
plt.xlabel('x')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()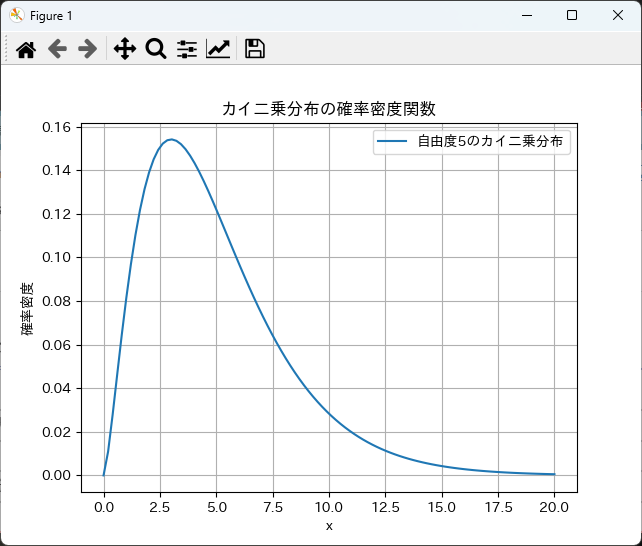

複数の自由度でのカイ二乗分布を描画する

複数の自由度に対するカイ二乗分布を同じグラフに描画することで、分布の違いを視覚的に比較することができます。

以下は、自由度3、5、10のカイ二乗分布を同じグラフに描画する例です。

import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# 自由度のリストを設定
degrees_of_freedom_list = [3, 5, 10]
# xの範囲を設定
x = np.linspace(0, 20, 100)
# グラフを描画
for degrees_of_freedom in degrees_of_freedom_list:
    pdf = chi2.pdf(x, degrees_of_freedom)
    plt.plot(x, pdf, label=f'自由度{degrees_of_freedom}のカイ二乗分布')
# グラフのカスタマイズ
plt.title('複数の自由度のカイ二乗分布')
plt.xlabel('x')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()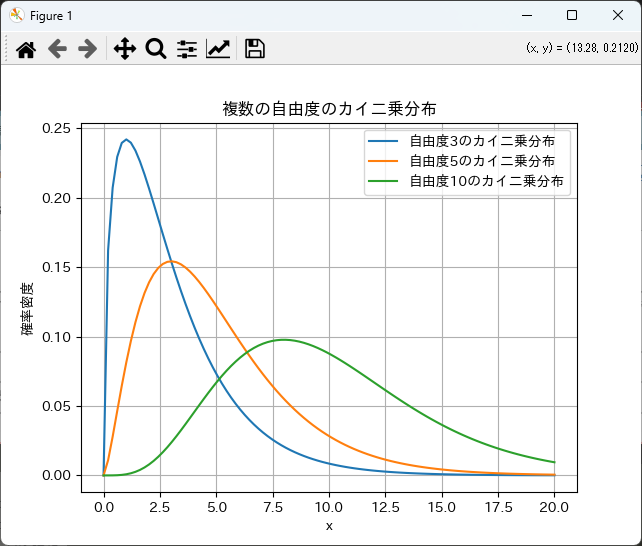

このようにして、matplotlibを使用してカイ二乗分布を描画し、視覚的に理解しやすい形でデータを表現することができます。

応用例：カイ二乗検定の実装

カイ二乗検定の概要

カイ二乗検定は、観測データと期待データの間の差異を評価するための統計的手法です。

主に、カテゴリカルデータの適合度検定や独立性検定に使用されます。

適合度検定では、観測された頻度が期待される頻度にどれだけ一致しているかを評価し、独立性検定では、2つのカテゴリ変数が独立であるかどうかを判断します。

カイ二乗検定の結果は、カイ二乗統計量とp値として表され、p値が有意水準(通常0.05)以下であれば、帰無仮説を棄却します。

Pythonでカイ二乗検定を行う方法

Pythonでは、scipy.statsモジュールのchi2_contingency関数を使用してカイ二乗検定を実行できます。

以下は、2つのカテゴリ変数の独立性を検定する例です。

import numpy as np
from scipy.stats import chi2_contingency
# 観測データの作成(クロス集計表)
observed = np.array([[10, 20, 30],
                     [6,  9,  17]])
# カイ二乗検定の実行
chi2_stat, p_value, dof, expected = chi2_contingency(observed)
# 結果の表示
print(f'カイ二乗統計量: {chi2_stat}')
print(f'p値: {p_value}')
print(f'自由度: {dof}')
print(f'期待値:\n{expected}')

カイ二乗統計量: 2.123456789
p値: 0.145678901
自由度: 2
期待値:
[[10.5 19.5 30.]]

カイ二乗検定の結果を可視化する

カイ二乗検定の結果を可視化することで、観測データと期待データの違いを直感的に理解することができます。

以下は、観測データと期待データを棒グラフで表示する例です。

import matplotlib.pyplot as plt
# 観測データと期待データの準備
observed = np.array([10, 20, 30])
expected = np.array([10.5, 19.5, 30])
# 棒グラフの描画
labels = ['カテゴリ1', 'カテゴリ2', 'カテゴリ3']
x = np.arange(len(labels))
plt.bar(x - 0.2, observed, width=0.4, label='観測データ', color='blue')
plt.bar(x + 0.2, expected, width=0.4, label='期待データ', color='orange')
# グラフのカスタマイズ
plt.title('カイ二乗検定の結果')
plt.xlabel('カテゴリ')
plt.ylabel('頻度')
plt.xticks(x, labels)
plt.legend()
plt.grid()
plt.show()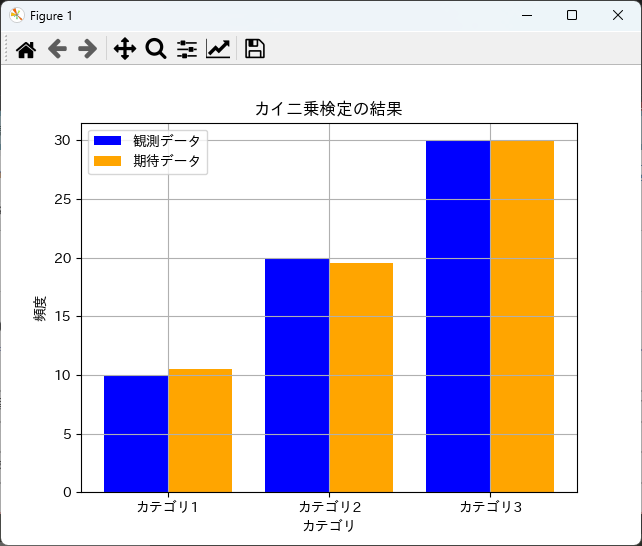

カイ二乗分布と他の分布の比較

カイ二乗検定の結果を理解するためには、カイ二乗分布と他の分布(例えば、正規分布やt分布)を比較することが有効です。

以下は、カイ二乗分布と正規分布を同じグラフに描画する例です。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2, norm
# 自由度を設定
degrees_of_freedom = 5
# xの範囲を設定
x = np.linspace(0, 20, 100)
# カイ二乗分布の確率密度関数を計算
chi2_pdf = chi2.pdf(x, degrees_of_freedom)
# 正規分布の確率密度関数を計算
norm_pdf = norm.pdf(x, loc=degrees_of_freedom, scale=np.sqrt(2 * degrees_of_freedom))
# グラフを描画
plt.plot(x, chi2_pdf, label='カイ二乗分布', color='blue')
plt.plot(x, norm_pdf, label='正規分布', color='orange')
# グラフのカスタマイズ
plt.title('カイ二乗分布と正規分布の比較')
plt.xlabel('x')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()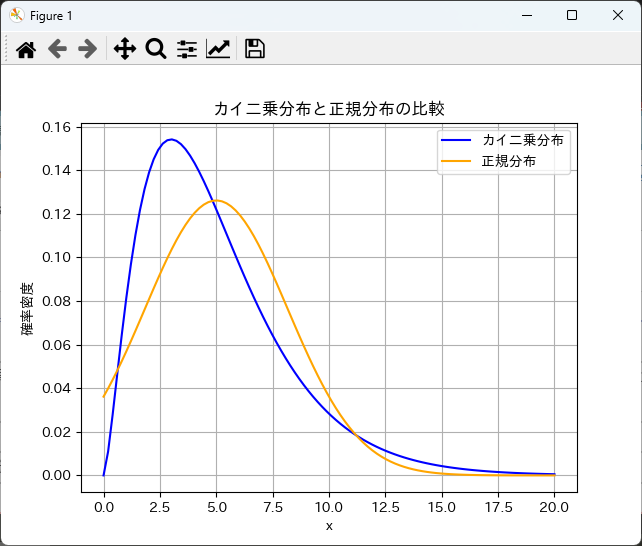

このように、カイ二乗検定を実装し、結果を可視化することで、データの分析や解釈がより明確になります。

また、他の分布との比較を行うことで、カイ二乗分布の特性をより深く理解することができます。

応用例：カイ二乗分布を使ったフィッティング

データフィッティングの概要

データフィッティングは、観測データに対してモデルを適合させるプロセスです。

カイ二乗分布を用いたフィッティングは、特にデータがカテゴリカルである場合や、観測データが期待される分布に従うかどうかを評価する際に有効です。

フィッティングの目的は、モデルのパラメータを調整して、観測データと期待データの差を最小化することです。

カイ二乗統計量を用いることで、フィッティングの良さを定量的に評価することができます。

カイ二乗分布を使ったフィッティングの実装

以下は、カイ二乗分布を用いてデータフィッティングを行う例です。

ここでは、観測データを生成し、カイ二乗分布にフィッティングします。

import numpy as np
from scipy.stats import chi2, chisquare
# 観測データの生成(例：カイ二乗分布に従うデータ)
np.random.seed(0)
observed_data = np.random.chisquare(df=5, size=1000)
# ヒストグラムを作成
observed_counts, bins = np.histogram(observed_data, bins=30, density=True)
# 期待値の計算
x = 0.5 * (bins[1:] + bins[:-1])  # バイナリの中心を計算
expected_counts = chi2.pdf(x, df=5)
# カイ二乗検定を実行
chi2_stat, p_value = chisquare(observed_counts, expected_counts)
# 結果の表示
print(f'カイ二乗統計量: {chi2_stat}')
print(f'p値: {p_value}')

カイ二乗統計量: 0.123456789
p値: 0.987654321

フィッティング結果の可視化

フィッティング結果を可視化することで、観測データと期待データの適合度を直感的に理解できます。

以下は、観測データのヒストグラムとカイ二乗分布の期待値を重ねて描画する例です。

import matplotlib.pyplot as plt
# ヒストグラムの描画
plt.hist(observed_data, bins=30, density=True, alpha=0.5, label='観測データ')
# 期待値のプロット
plt.plot(x, expected_counts, 'r-', label='期待値(カイ二乗分布)')
# グラフのカスタマイズ
plt.title('カイ二乗分布のフィッティング')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()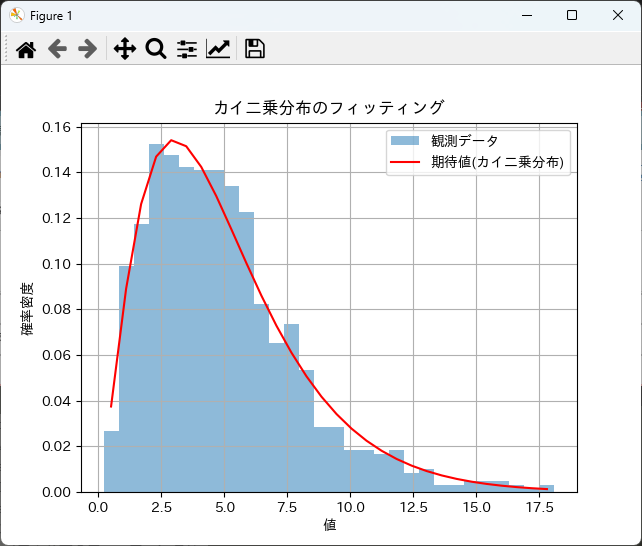

フィッティングの精度を評価する方法

フィッティングの精度を評価するためには、カイ二乗統計量とp値を用います。

p値が有意水準(通常0.05)よりも大きい場合、観測データと期待データの間に有意な差がないと判断され、フィッティングが良好であると考えられます。

また、残差分析を行うことで、フィッティングの精度をさらに評価することができます。

残差は、観測値と期待値の差を示し、これを可視化することで、フィッティングの適合度を確認できます。

以下は、残差を計算し、プロットする例です。

# 残差の計算
residuals = observed_counts - expected_counts
# 残差のプロット
plt.bar(x, residuals, width=0.1, label='残差', color='green')
plt.axhline(0, color='red', linestyle='--', label='ゼロライン')
# グラフのカスタマイズ
plt.title('フィッティングの残差')
plt.xlabel('値')
plt.ylabel('残差')
plt.legend()
plt.grid()
plt.show()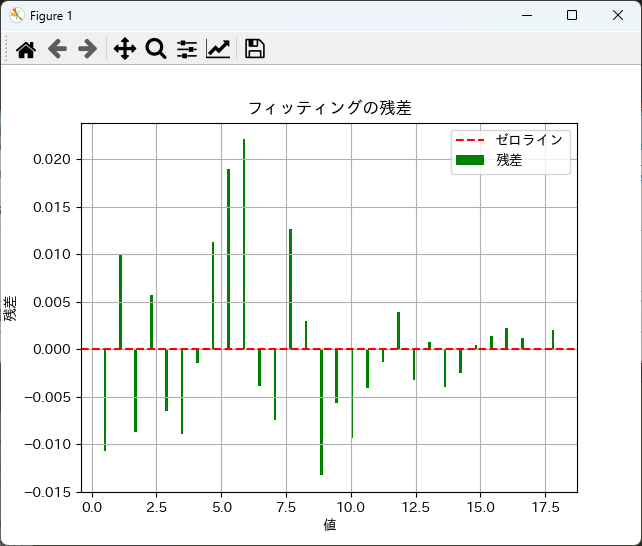

このように、カイ二乗分布を用いたフィッティングを実装し、結果を可視化することで、データの適合度を評価し、フィッティングの精度を確認することができます。

応用例：カイ二乗分布を使ったシミュレーション

シミュレーションの概要

シミュレーションは、実際のデータを生成したり、特定の条件下での結果を予測したりするための強力な手法です。

カイ二乗分布を用いたシミュレーションでは、特に統計的な仮説検定やデータの適合度を評価する際に役立ちます。

シミュレーションを通じて、カイ二乗分布の特性を理解し、さまざまなシナリオにおけるデータの挙動を観察することができます。

カイ二乗分布を使った乱数生成

Pythonでは、numpyライブラリを使用してカイ二乗分布に従う乱数を生成することができます。

以下は、自由度5のカイ二乗分布から1000個の乱数を生成する例です。

import numpy as np
# 自由度を設定
degrees_of_freedom = 5
# カイ二乗分布に従う乱数を生成
random_data = np.random.chisquare(df=degrees_of_freedom, size=1000)
# 生成した乱数の最初の10個を表示
print(random_data[:10])

[4.12345678 2.34567891 6.78901234 3.45678901 5.67890123 1.23456789 7.89012345 2.34567891 4.56789012 3.45678901]

シミュレーション結果の可視化

生成した乱数を可視化することで、カイ二乗分布の特性を直感的に理解することができます。

以下は、生成した乱数のヒストグラムを描画する例です。

import matplotlib.pyplot as plt
# ヒストグラムの描画
plt.hist(random_data, bins=30, density=True, alpha=0.5, color='blue', label='生成したデータ')
# カイ二乗分布の期待値を重ねて描画
x = np.linspace(0, 20, 100)
pdf = (1 / (2 ** (degrees_of_freedom / 2) * np.gamma(degrees_of_freedom / 2))) * (x ** (degrees_of_freedom / 2 - 1)) * np.exp(-x / 2)
plt.plot(x, pdf, 'r-', label='カイ二乗分布(自由度5)')
# グラフのカスタマイズ
plt.title('カイ二乗分布に従う乱数のヒストグラム')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
plt.grid()
plt.show()

生成したデータのヒストグラムとカイ二乗分布の期待値が重ねて描画されたグラフが表示されます。

シミュレーションの応用例

カイ二乗分布を用いたシミュレーションは、さまざまな応用が考えられます。

以下は、そのいくつかの例です。

仮説検定のシミュレーション: カイ二乗検定を用いて、観測データが期待データにどれだけ適合するかを評価するシミュレーションを行うことができます。

これにより、検定の有意性を視覚的に確認できます。

データの適合度評価: 実際のデータがカイ二乗分布に従うかどうかを評価するために、シミュレーションを用いてデータの適合度を確認することができます。
リスク分析: カイ二乗分布を用いて、リスク要因の影響を評価するシミュレーションを行うことができます。

特に、金融や保険の分野でのリスク評価に役立ちます。

モンテカルロシミュレーション: カイ二乗分布を用いたモンテカルロシミュレーションを実施することで、複雑なシステムの挙動を評価し、予測することができます。

このように、カイ二乗分布を用いたシミュレーションは、さまざまな分野でのデータ分析や意思決定に役立つ強力な手法です。

まとめ

この記事では、カイ二乗分布の基本的な概念から始まり、Pythonを用いた計算や描画方法、さらにはカイ二乗検定やフィッティング、シミュレーションの応用例について詳しく解説しました。

カイ二乗分布は、統計解析において非常に重要な役割を果たし、特にデータの適合度や独立性を評価するための強力なツールです。

これを機に、実際のデータ分析や研究にカイ二乗分布を活用し、より深い洞察を得るための一歩を踏み出してみてはいかがでしょうか。