[Python] ベッセル関数を使ったグラフ作成方法
Pythonでベッセル関数を使ったグラフを作成するには、scipyライブラリのscipy.special.jn関数を使用し、matplotlibでグラフを描画します。
jn(n, x)はベッセル関数の第1種を表し、nは次数、xは引数です。
まず、numpyでx軸の値を生成し、次にscipy.special.jnでベッセル関数の値を計算し、最後にmatplotlib.pyplot.plotでグラフを描画します。
ベッセル関数とは
ベッセル関数は、特に円筒対称の問題において重要な役割を果たす特殊関数です。
物理学や工学の多くの分野で現れるこの関数は、波動、熱伝導、電磁場の解析などに利用されます。
ベッセル関数には主に第1種と第2種があり、これらはそれぞれ異なる境界条件に基づいて定義されます。
ベッセル関数の一般的な形は、次のように表されます:
\[J_n(x) = \sum_{k=0}^{\infty} \frac{(-1)^k}{k! , \Gamma(n+k+1)} \left( \frac{x}{2} \right)^{n+2k}\]
ここで、\(J_n(x)\)は第n次のベッセル関数、\(\Gamma\)はガンマ関数を示します。
ベッセル関数は、特に振動や波動の解析において、非常に重要な数学的ツールです。
Pythonでベッセル関数を計算する方法
scipy.specialモジュールのインストール方法
Pythonでベッセル関数を計算するためには、scipyライブラリが必要です。
scipyは科学技術計算のためのライブラリで、specialモジュールにはベッセル関数が含まれています。
以下のコマンドを使用して、scipyをインストールできます。
pip install scipyscipy.special.jn関数の使い方
scipy.special.jn関数を使用すると、第1種のベッセル関数を計算できます。
以下は、ベッセル関数を計算するサンプルコードです。
import numpy as np
from scipy.special import jn
import matplotlib.pyplot as plt
# xの値を生成
x = np.linspace(0, 20, 100)
# 第0次のベッセル関数を計算
y0 = jn(0, x)
# グラフの描画
plt.plot(x, y0, label='J0(x)')
plt.title('第0次のベッセル関数')
plt.xlabel('x')
plt.ylabel('J0(x)')
plt.legend()
plt.grid()
plt.show()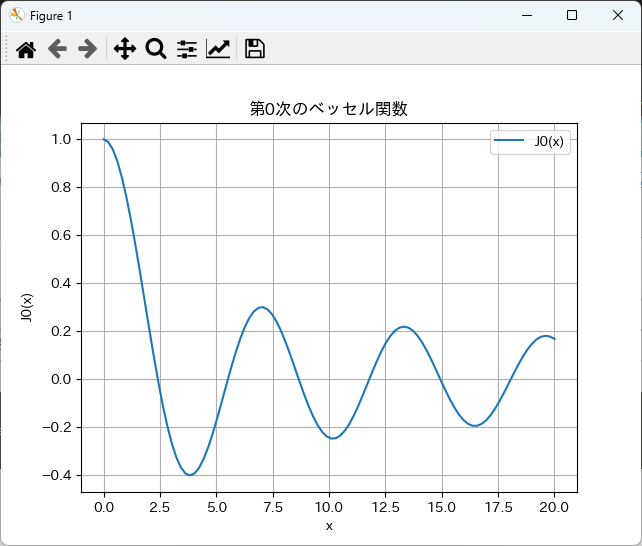
出力結果は、xの範囲における第0次のベッセル関数のグラフです。
ベッセル関数の第1種と第2種の違い
ベッセル関数には第1種と第2種の2種類があります。
主な違いは以下の通りです。
| 特徴 | 第1種ベッセル関数 \(J_n(x)\) | 第2種ベッセル関数 \(Y_n(x)\) |
|---|---|---|
| 定義 | 有限の値を持つ | 無限大の値を持つ |
| 境界条件 | 円筒対称の問題に適用 | 特定の境界条件に適用 |
| 使用例 | 振動、波動の解析 | 電磁場の解析 |
高次のベッセル関数の計算方法
高次のベッセル関数もscipy.special.jn関数を使用して計算できます。
例えば、第3次のベッセル関数を計算する場合は、次のようにします。
# 第3次のベッセル関数を計算
y3 = jn(3, x)
# グラフの描画
plt.plot(x, y3, label='J3(x)', color='orange')
plt.title('第3次のベッセル関数')
plt.xlabel('x')
plt.ylabel('J3(x)')
plt.legend()
plt.grid()
plt.show()このコードを実行すると、第3次のベッセル関数のグラフが表示されます。
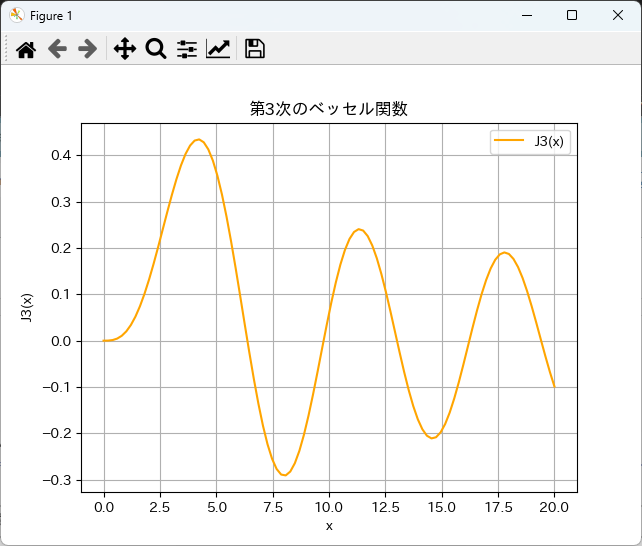
高次のベッセル関数も同様に計算でき、さまざまな物理現象の解析に役立ちます。
ベッセル関数のグラフを作成する手順
必要なライブラリのインポート
ベッセル関数のグラフを作成するためには、以下のライブラリをインポートします。
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jnx軸の値を生成する方法 (numpyの使用)
numpyを使用して、x軸の値を生成します。
例えば、0から20までの範囲で100個の等間隔の値を生成するには、次のようにします。
# xの値を生成
x = np.linspace(0, 20, 100)ベッセル関数の値を計算する方法
生成したxの値を使って、ベッセル関数の値を計算します。
ここでは、第0次のベッセル関数を計算します。
# 第0次のベッセル関数を計算
y0 = jn(0, x)matplotlibを使ったグラフの描画
matplotlibを使用して、計算したベッセル関数の値をグラフに描画します。
以下のコードでグラフを描画できます。
# グラフの描画
plt.plot(x, y0, label='J0(x)')
plt.title('第0次のベッセル関数')
plt.xlabel('x')
plt.ylabel('J0(x)')
plt.grid()
plt.show()グラフのカスタマイズ(タイトル、軸ラベル、凡例の追加)
グラフをより見やすくするために、タイトル、軸ラベル、凡例を追加します。
上記のコードに含まれているplt.title、plt.xlabel、plt.ylabel、plt.legendを使用して、これらを設定します。
以下は、カスタマイズされたグラフの例です。
# グラフの描画
plt.plot(x, y0, label='J0(x)', color='blue')
plt.title('第0次のベッセル関数のグラフ')
plt.xlabel('xの値')
plt.ylabel('J0(x)の値')
plt.axhline(0, color='black', lw=0.5, ls='--') # x軸
plt.axvline(0, color='black', lw=0.5, ls='--') # y軸
plt.legend()
plt.grid()
plt.show()このようにして、ベッセル関数のグラフを作成し、視覚的にわかりやすくカスタマイズすることができます。
複数のベッセル関数を同時に描画する
複数の次数のベッセル関数を計算する
複数の次数のベッセル関数を計算するためには、scipy.special.jn関数を使用して、異なる次数のベッセル関数をそれぞれ計算します。
以下のコードでは、第0次、第1次、第2次のベッセル関数を計算します。
import numpy as np
from scipy.special import jn
# xの値を生成
x = np.linspace(0, 20, 100)
# 複数の次数のベッセル関数を計算
y0 = jn(0, x) # 第0次
y1 = jn(1, x) # 第1次
y2 = jn(2, x) # 第2次複数のベッセル関数を1つのグラフに描画する
計算した複数のベッセル関数を1つのグラフに描画するには、plt.plotを複数回呼び出します。
以下のコードでは、3つのベッセル関数を同じグラフに描画します。
import matplotlib.pyplot as plt
# グラフの描画
plt.plot(x, y0, label='J0(x)', color='blue')
plt.plot(x, y1, label='J1(x)', color='orange')
plt.plot(x, y2, label='J2(x)', color='green')
# グラフのカスタマイズ
plt.title('複数のベッセル関数のグラフ')
plt.xlabel('xの値')
plt.ylabel('J_n(x)の値')
plt.axhline(0, color='black', lw=0.5, ls='--') # x軸
plt.axvline(0, color='black', lw=0.5, ls='--') # y軸
plt.grid()
plt.legend()
plt.show()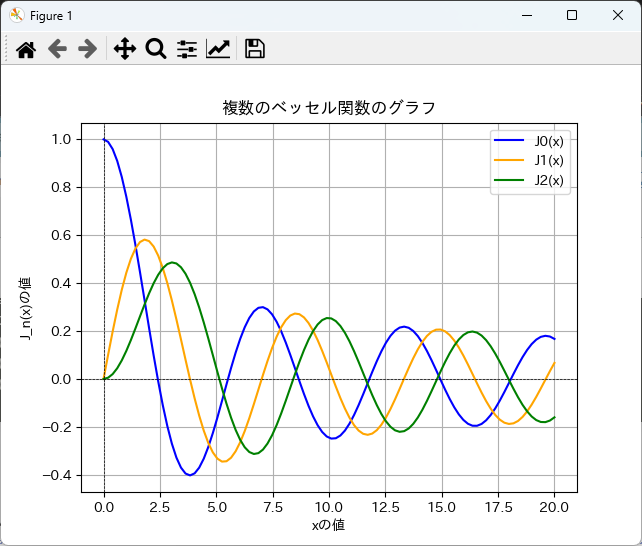
グラフの色やスタイルを変更する方法
グラフの色やスタイルを変更するには、plt.plotの引数を使用します。
色はcolor引数で指定し、線のスタイルはlinestyle引数で指定できます。
以下の例では、異なるスタイルを使用しています。
# グラフの描画
plt.plot(x, y0, label='J0(x)', color='blue', linestyle='-') # 実線
plt.plot(x, y1, label='J1(x)', color='orange', linestyle='--') # 破線
plt.plot(x, y2, label='J2(x)', color='green', linestyle=':') # 点線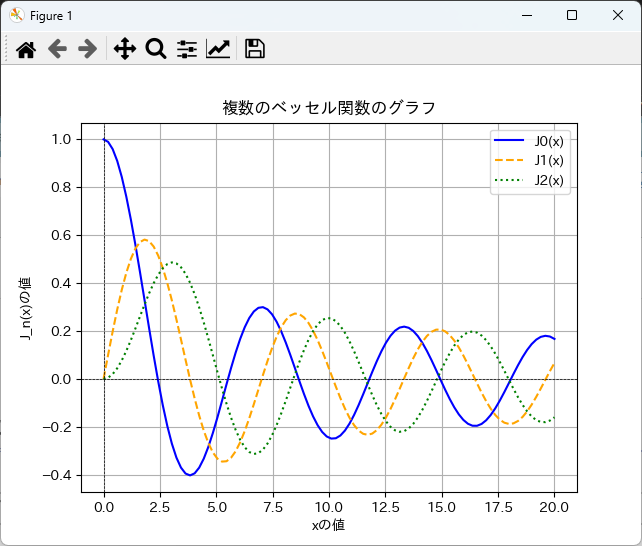
応用例:ベッセル関数を使った物理シミュレーション
波動方程式におけるベッセル関数の利用
波動方程式は、波の伝播を記述する基本的な方程式であり、特に円筒対称の問題においてはベッセル関数が重要な役割を果たします。
円筒座標系での波動方程式は、次のように表されます。
\[\frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partial u}{\partial r} \right) + \frac{1}{r^2} \frac{\partial^2 u}{\partial \theta^2} + \frac{\partial^2 u}{\partial z^2} = 0\]
ここで、\(u\)は波の振幅、\(r\)は半径、\(\theta\)は角度、\(z\)は高さを示します。
この方程式の解は、ベッセル関数を用いて表現され、特に円筒形の波動の解析に利用されます。
振動現象のシミュレーション
ベッセル関数は、振動現象のシミュレーションにも利用されます。
例えば、円形の膜の振動を考えると、膜の振動モードはベッセル関数によって記述されます。
膜の振動は、次のような形で表されます。
\[u(r, t) = J_n(kr) \cos(\omega t)\]
ここで、\(J_n\)は第n次のベッセル関数、\(k\)は波数、\(\omega\)は角周波数を示します。
この式を用いることで、膜の振動の時間的変化をシミュレーションすることができます。
電磁波の伝播におけるベッセル関数の応用
電磁波の伝播においても、ベッセル関数は重要な役割を果たします。
特に、円筒形の導体や光ファイバー内での電磁波の伝播は、ベッセル関数を用いて解析されます。
マクスウェル方程式を解くことで、電磁波の伝播モードは次のように表されます。
\[E(r, \theta, z) = J_n(kr) e^{i(n\theta – \beta z)}\]
ここで、\(E\)は電場の強度、\(\beta\)は伝播定数を示します。
このように、ベッセル関数を用いることで、円筒形の構造内での電磁波の挙動を詳細に解析することが可能です。
これらの応用例からもわかるように、ベッセル関数は物理シミュレーションにおいて非常に重要な役割を果たしており、さまざまな現象の理解や解析に貢献しています。
応用例:ベッセル関数を使ったデータフィッティング
実データにベッセル関数をフィットさせる方法
実データにベッセル関数をフィットさせることで、データの背後にある物理的な現象を理解することができます。
例えば、実験データがベッセル関数の形状に従っている場合、ベッセル関数を用いてデータをモデル化し、パラメータを推定することができます。
フィッティングの一般的な手順は以下の通りです。
- 実データを収集する。
- フィッティングに使用するベッセル関数の次数を決定する。
- 初期パラメータを設定する。
- フィッティングを実行し、最適なパラメータを求める。
scipy.optimize.curve_fitを使ったフィッティング
scipy.optimize.curve_fit関数を使用すると、データにベッセル関数をフィットさせることができます。
以下は、実データに第0次のベッセル関数をフィットさせるサンプルコードです。
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jn
from scipy.optimize import curve_fit
# 実データの生成(例としてノイズを含むデータ)
x_data = np.linspace(0, 20, 50)
y_data = jn(0, x_data) + np.random.normal(0, 0.1, x_data.size) # ノイズを加えたデータ
# ベッセル関数の定義
def bessel_func(x, a, b):
return a * jn(0, b * x)
# フィッティングの実行
initial_guess = [1, 1] # 初期パラメータ
params, covariance = curve_fit(bessel_func, x_data, y_data, p0=initial_guess)
# フィッティング結果のパラメータ
a_fit, b_fit = params
print(f'フィッティング結果: a = {a_fit}, b = {b_fit}')フィッティング結果の可視化
フィッティング結果を可視化することで、実データとフィッティングしたベッセル関数の適合度を確認できます。
以下のコードでは、実データとフィッティング結果を同じグラフに描画します。
# フィッティング結果の計算
y_fit = bessel_func(x_data, a_fit, b_fit)
# グラフの描画
plt.scatter(x_data, y_data, label='実データ', color='red', marker='o')
plt.plot(x_data, y_fit, label='フィッティング結果', color='blue')
plt.title('ベッセル関数によるデータフィッティング')
plt.xlabel('xの値')
plt.ylabel('yの値')
plt.axhline(0, color='black', lw=0.5, ls='--') # x軸
plt.axvline(0, color='black', lw=0.5, ls='--') # y軸
plt.legend()
plt.grid()
plt.show()このようにして、実データにベッセル関数をフィットさせ、その結果を可視化することができます。
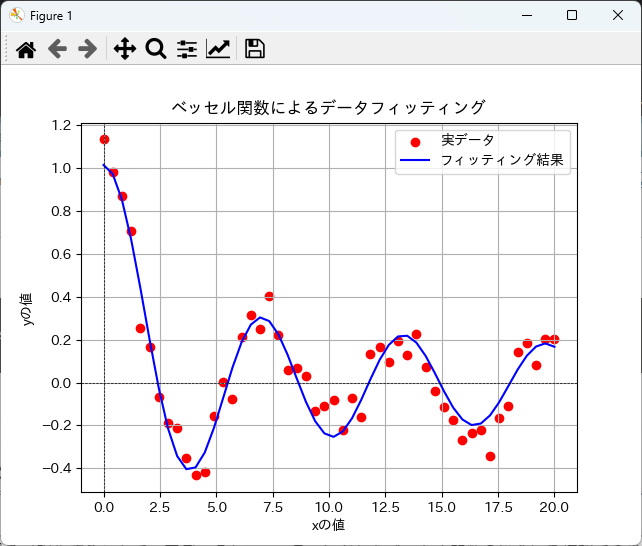
データフィッティングは、実験データの解析やモデルの検証において非常に有用な手法です。
応用例:ベッセル関数を使った信号処理
フィルタ設計におけるベッセル関数の利用
信号処理において、フィルタ設計は非常に重要な役割を果たします。
特に、ベッセルフィルタは、位相特性が優れているため、オーディオ信号や画像処理などのアプリケーションで広く使用されています。
ベッセルフィルタは、信号の位相を保持しながら、特定の周波数成分を通過させることができるため、信号の歪みを最小限に抑えることができます。
ベッセルフィルタは、次のような特性を持っています:
- 平坦な位相応答:信号の位相を保持し、遅延を最小限に抑える。
- 滑らかな周波数応答:周波数特性が滑らかで、急激な変化がない。
ベッセルフィルタの特性とその実装
ベッセルフィルタは、一般的に低域通過フィルタとして設計されます。
以下は、Pythonを使用してベッセルフィルタを実装するサンプルコードです。
scipy.signalモジュールを使用して、ベッセルフィルタの係数を計算し、信号に適用します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import bessel, lfilter
# サンプリング周波数とカットオフ周波数
fs = 1000 # サンプリング周波数 (Hz)
fc = 100 # カットオフ周波数 (Hz)
# ベッセルフィルタの設計
order = 4 # フィルタの次数
b, a = bessel(order, fc / (0.5 * fs), btype='low', analog=False)
# 信号の生成(サイン波 + ノイズ)
t = np.linspace(0, 1, fs, endpoint=False)
signal = np.sin(2 * np.pi * 50 * t) + 0.5 * np.random.normal(size=t.shape)
# フィルタの適用
filtered_signal = lfilter(b, a, signal)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(t, signal, label='元の信号', color='red', alpha=0.5)
plt.plot(t, filtered_signal, label='ベッセルフィルタ後の信号', color='blue')
plt.title('ベッセルフィルタによる信号処理')
plt.xlabel('時間 (秒)')
plt.ylabel('振幅')
plt.legend()
plt.grid()
plt.show()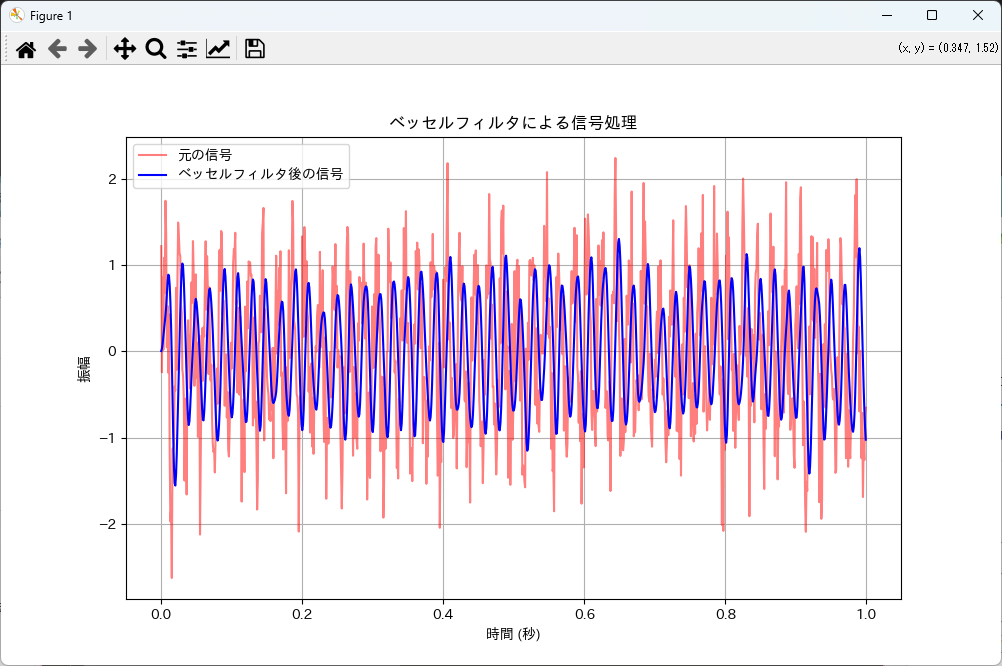
信号処理におけるベッセル関数の利点
ベッセル関数を用いた信号処理には、いくつかの利点があります。
- 位相の保持:ベッセルフィルタは、信号の位相を保持するため、信号の歪みを最小限に抑えることができます。
これにより、オーディオ信号や画像処理において、より自然な結果が得られます。
- 滑らかな応答:周波数応答が滑らかであるため、信号の急激な変化を避けることができ、フィルタリング後の信号がより滑らかになります。
- 高い安定性:ベッセルフィルタは、他のフィルタと比較して安定性が高く、特に高次のフィルタでも安定した動作を示します。
これらの特性により、ベッセル関数は信号処理において非常に有用なツールとなっています。
特に、音声や画像の処理において、信号の品質を保ちながら必要な成分を抽出するために広く利用されています。
まとめ
この記事では、ベッセル関数の基本的な概念から、Pythonを用いた計算方法、グラフ作成の手順、さらには物理シミュレーションやデータフィッティング、信号処理における応用例まで幅広く取り上げました。
ベッセル関数は、特に円筒対称の問題において重要な役割を果たし、さまざまな分野での解析やシミュレーションに利用されています。
これを機に、実際のデータや問題にベッセル関数を適用し、より深い洞察を得るための実践を始めてみてはいかがでしょうか。

![[Python] deapライブラリの使い方 – 遺伝的アルゴリズム](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46601.png)
![[Python] bisectライブラリの使い方 – ニ分探索の効率化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46600.png)
![[Python] a*(A Star)探索アルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43234.png)
![[Python] ベジェ曲線を実装する方法(二次ベジェ/三次ベジェ)](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43239.png)
![[Python] ベルヌーイ分布を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43237.png)
![[Python] エイトケンのΔ2乗加速法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43236.png)
![[Python] アッカーマン関数のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43235.png)
![[Python] matplotlibでC曲線を描画する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43245.png)
![[Python] CRC(巡回冗長検査)のアルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43244.png)
![[Python] コラッツ予想(コラッツの問題)のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43243.png)
![[Python] コーシー分布の計算を行う方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43242.png)
![[Python] ボイヤームーア法で文字列検索する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43240.png)