[C言語] Mandelbrot集合の描画方法とアルゴリズム解説

Mandelbrot集合は複素数平面上の点の集合で、特定の条件を満たす複素数cに対して生成されます。

描画には、各点cに対して反復計算を行い、特定の条件を満たすかどうかを確認します。

具体的には、z = z^2 + cという式を初期値z=0から繰り返し計算し、|z|が2を超えるか、最大反復回数に達するまで続けます。

|z|が2を超えた場合、その点は集合に含まれません。

C言語では、2重ループを用いて複素数平面上の各点を評価し、結果に基づいてピクセルを描画します。

色付けは反復回数に基づいて行われ、視覚的に美しいフラクタルパターンを生成します。

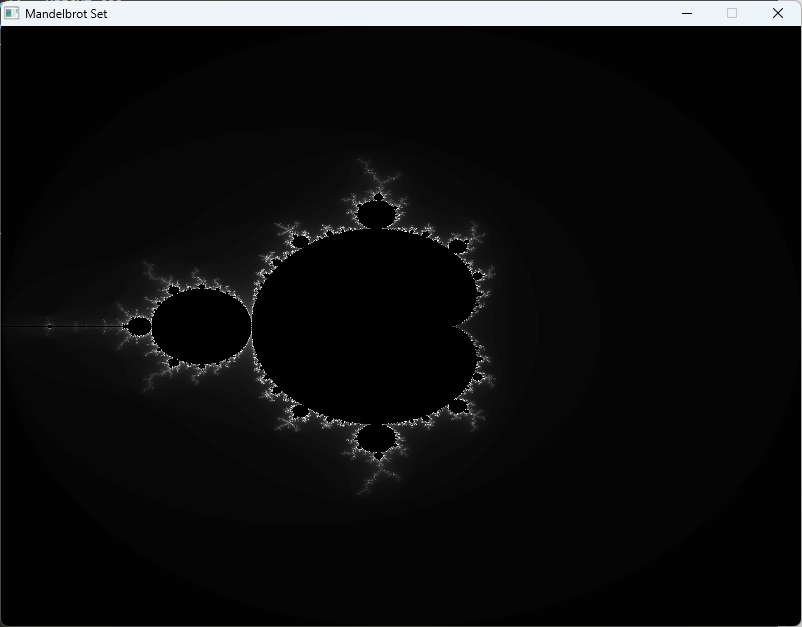
Mandelbrot集合とは

Mandelbrot集合は、数学とコンピュータサイエンスの分野で非常に興味深い対象です。

この集合は、複雑な数の平面上で特定の条件を満たす点の集合として定義され、視覚的に非常に美しいフラクタルパターンを形成します。

以下では、Mandelbrot集合の定義、フラクタルの基本、そして複素数平面との関係について詳しく説明します。

Mandelbrot集合の定義

Mandelbrot集合は、複素数 ( c ) に対して、次の反復関数を用いて定義されます。

ここで、初期条件として ( z_0 = 0 ) を設定します。

Mandelbrot集合は、この反復関数が無限に続けられたときに発散しない複素数 ( c ) の集合です。

具体的には、反復の結果がある一定の境界を超えない場合、その ( c ) はMandelbrot集合に属します。

フラクタルの基本

フラクタルとは、自己相似性を持つ複雑なパターンのことを指します。

自己相似性とは、部分が全体と似た形状を持つ性質です。

Mandelbrot集合は、ズームインしても同様のパターンが繰り返し現れるという特徴を持ち、典型的なフラクタルの例とされています。

フラクタルの性質は、自然界の多くの現象に見られ、例えば、海岸線の形状や雪の結晶などが挙げられます。

Mandelbrot集合は、数学的に定義されたフラクタルであり、その美しさと複雑さから多くの研究者やアーティストに影響を与えています。

複素数平面とMandelbrot集合

複素数平面は、実数軸と虚数軸からなる2次元の平面です。

Mandelbrot集合は、この複素数平面上で定義され、各点が特定の条件を満たすかどうかによって集合に含まれるかが決まります。

具体的には、複素数 ( c = a + bi ) の実部 ( a ) と虚部 ( b ) を平面上の座標として考えます。

Mandelbrot集合は、この平面上で反復関数が発散しない点の集合として視覚化されます。

視覚化されたMandelbrot集合は、黒い領域が集合に属する点を示し、色付きの領域が発散する点を示します。

このように、Mandelbrot集合は数学的な定義に基づき、複素数平面上で美しいフラクタルパターンを形成します。

次のセクションでは、この集合を描画するためのアルゴリズムについて詳しく解説します。

Mandelbrot集合の数学的背景

Mandelbrot集合を理解するためには、複素数や反復関数の概念をしっかりと把握することが重要です。

ここでは、Mandelbrot集合の数学的背景として、複素数の基本、反復関数の説明、そして発散と収束の条件について詳しく解説します。

複素数の基本

複素数は、実数と虚数を組み合わせた数で、通常 ( z = a + bi ) の形で表されます。

ここで、( a ) は実部、( b ) は虚部、( i ) は虚数単位であり、( i^2 = -1 ) という性質を持ちます。

複素数は、2次元の平面上で表現され、実部が横軸、虚部が縦軸に対応します。

この平面を複素数平面と呼びます。

複素数の演算には、加算、減算、乗算、除算があり、特に乗算は回転と拡大縮小を表すことができます。

反復関数の説明

Mandelbrot集合の定義に用いられる反復関数は、次のように表されます。

ここで、( z_0 = 0 ) から始め、複素数 ( c ) を定数として、反復を繰り返します。

この反復関数は、各ステップで現在の値を二乗し、定数 ( c ) を加える操作を行います。

この反復の結果が発散するか収束するかによって、複素数 ( c ) がMandelbrot集合に属するかどうかが決まります。

発散する場合、反復の結果が無限大に向かって増加し、収束する場合はある有限の値に近づきます。

発散と収束の条件

Mandelbrot集合において、反復関数が発散するか収束するかを判断するための条件があります。

一般的に、反復の結果がある一定の境界を超えると発散するとみなされます。

具体的には、反復の結果 ( ) の絶対値が2を超えた場合、その複素数 ( c ) は発散すると判断されます。

これは、絶対値が2を超えると、次の反復で指数的に増加する可能性が高いためです。

この条件を用いて、Mandelbrot集合に属するかどうかを判定することができます。

収束する場合、反復の結果は境界を超えず、Mandelbrot集合に属することになります。

以上のように、Mandelbrot集合の数学的背景には、複素数の基本的な性質と反復関数の挙動が深く関わっています。

次のセクションでは、これらの知識を基にMandelbrot集合を描画するアルゴリズムについて解説します。

Mandelbrot集合の描画アルゴリズム

Mandelbrot集合を描画するためには、複素数の反復計算を行い、その結果に基づいて各点の色を決定するアルゴリズムが必要です。

ここでは、基本的なアルゴリズムの流れから、反復計算の実装、発散判定の方法、そしてSDLを用いた完成したプログラムについて解説します。

基本的なアルゴリズムの流れ

Mandelbrot集合の描画アルゴリズムは、以下のような流れで進行します。

1. 描画領域を設定し、各ピクセルに対応する複素数 ( c ) を決定する。
2. 各ピクセルについて、反復計算を行い、発散するかどうかを判定する。
3. 発散の速さに基づいてピクセルの色を決定する。
4. 全てのピクセルについて計算を行い、画像を生成する。

このアルゴリズムにより、複素数平面上の各点がMandelbrot集合に属するかどうかを視覚的に表現できます。

反復計算の実装

反復計算は、次の式に基づいて行われます。

初期条件として ( ) を設定し、指定された最大反復回数まで計算を繰り返します。

以下にC言語での反復計算の実装例を示します。

#include <complex.h>
int mandelbrot(complex double c, int max_iter) {
    complex double z = 0;
    int n = 0;
    while (cabs(z) <= 2 && n < max_iter) {
        z = z * z + c;
        n++;
    }
    return n;
}

発散判定の方法

発散判定は、反復計算の結果 ( ) の絶対値が2を超えたかどうかで行います。

絶対値が2を超えた時点で、その点は発散するとみなし、反復を終了します。

発散の速さ(反復回数)に基づいて色を決定することで、Mandelbrot集合の美しいパターンを描画できます。

完成したプログラム

以下に、SDLを用いてMandelbrot集合を描画するC言語のプログラムを示します。

#include <SDL2/SDL.h>
#include <complex.h>
#define WIDTH 800
#define HEIGHT 600
#define MAX_ITER 1000
int mandelbrot(complex double c, int max_iter) {
    complex double z = 0;
    int n = 0;
    while (cabs(z) <= 2 && n < max_iter) {
        z = z * z + c;
        n++;
    }
    return n;
}
int main(int argc, char *argv[]) {
    SDL_Init(SDL_INIT_VIDEO);
    SDL_Window *window =
        SDL_CreateWindow("Mandelbrot Set", SDL_WINDOWPOS_UNDEFINED,
                         SDL_WINDOWPOS_UNDEFINED, WIDTH, HEIGHT, 0);
    SDL_Renderer *renderer =
        SDL_CreateRenderer(window, -1, SDL_RENDERER_ACCELERATED);
    for (int y = 0; y < HEIGHT; y++) {
        for (int x = 0; x < WIDTH; x++) {
            double real = (x - WIDTH / 2.0) * 4.0 / WIDTH;
            double imag = (y - HEIGHT / 2.0) * 4.0 / HEIGHT;
            complex double c = real + imag * I;
            int n = mandelbrot(c, MAX_ITER);
            int color = (n == MAX_ITER) ? 0 : (255 * n * 10 / MAX_ITER);
            SDL_SetRenderDrawColor(renderer, color, color, color, 255);
            SDL_RenderDrawPoint(renderer, x, y);
        }
    }
    SDL_RenderPresent(renderer);
    SDL_Delay(5000);
    SDL_DestroyRenderer(renderer);
    SDL_DestroyWindow(window);
    SDL_Quit();
    return 0;
}

このプログラムは、SDLを用いてMandelbrot集合を描画します。

各ピクセルに対応する複素数を計算し、反復回数に基づいて色を設定します。

実行すると、ウィンドウにMandelbrot集合の画像が表示されます。

描画の最適化技術

Mandelbrot集合の描画は計算量が多く、特に高解像度での描画には時間がかかります。

ここでは、描画の効率を上げるための最適化技術について、計算速度の向上、メモリ使用量の削減、並列処理の導入という観点から解説します。

計算速度の向上

計算速度を向上させるための方法として、以下の技術が考えられます。

• エスケープタイムアルゴリズムの最適化: 発散判定の条件を早期に満たす場合、計算を打ち切ることで無駄な計算を省きます。

例えば、絶対値が2を超えた時点で即座にループを終了します。

• 固定小数点演算の利用: 複素数の計算において、浮動小数点演算の代わりに固定小数点演算を使用することで、計算速度を向上させることができます。

これは特にハードウェアの性能が限られている場合に有効です。

• ルックアップテーブルの使用: 特定の計算結果を事前にテーブルに格納し、必要に応じて再利用することで、計算を高速化します。

メモリ使用量の削減

メモリ使用量を削減するためには、以下の方法が有効です。

• データ型の選択: 必要以上に大きなデータ型を使用しないようにします。

例えば、色の情報を格納する際に、32ビットの整数ではなく8ビットの整数を使用することでメモリを節約できます。

• ピクセルデータの圧縮: 描画結果を圧縮形式で一時的に保存することで、メモリ使用量を削減します。

圧縮アルゴリズムを適用することで、メモリの消費を抑えることができます。

• メモリプールの利用: 頻繁に確保と解放を繰り返すメモリを、あらかじめ確保したメモリプールから管理することで、メモリの断片化を防ぎます。

並列処理の導入

並列処理を導入することで、描画の速度を大幅に向上させることができます。

以下にその方法を示します。

• マルチスレッド化: 各ピクセルの計算を独立したスレッドで処理することで、複数のCPUコアを活用し、描画速度を向上させます。

スレッドプールを使用することで、スレッドの管理を効率化できます。

• GPUの活用: GPUは並列計算に特化しており、Mandelbrot集合のような大量の独立した計算を高速に処理できます。

OpenCLやCUDAを使用して、GPUでの計算を実装することで、描画速度を劇的に向上させることが可能です。

• タイルベースのレンダリング: 画像を小さなタイルに分割し、それぞれを独立して計算することで、並列処理を効率的に行います。

これにより、キャッシュの効率も向上します。

これらの最適化技術を組み合わせることで、Mandelbrot集合の描画をより効率的に行うことができます。

次のセクションでは、これらの技術を応用した具体的な例について解説します。

応用例

Mandelbrot集合の描画技術は、さまざまな応用が可能です。

ここでは、カラーマッピングの応用、ズーム機能の実装、そして他のフラクタル集合への応用について解説します。

カラーマッピングの応用

Mandelbrot集合の描画において、カラーマッピングは視覚的な美しさを引き出す重要な要素です。

発散の速さに基づいて色を変えることで、より詳細で美しい画像を生成できます。

• グラデーションの使用: 発散回数に応じて色を滑らかに変化させることで、より自然で美しいグラデーションを実現します。

例えば、発散回数が少ないほど青色に近づけ、多いほど赤色に近づけるといった方法があります。

• カラーパレットのカスタマイズ: ユーザーがカラーパレットを選択できるようにすることで、個々の好みに応じたカラーマッピングを提供できます。

これにより、同じMandelbrot集合でも異なる印象を与えることができます。

• 周期的な色の変化: 発散回数を周期的に色にマッピングすることで、サイケデリックな効果を生み出すことができます。

これにより、視覚的に興味深いパターンを作成できます。

ズーム機能の実装

Mandelbrot集合の特徴の一つに、無限にズームインしても新たなパターンが現れるという性質があります。

ズーム機能を実装することで、この特性を活かしたインタラクティブな体験を提供できます。

• ズームインとズームアウト: ユーザーがクリックやスクロールでズームイン・ズームアウトできるようにすることで、Mandelbrot集合の詳細な構造を探索できます。

ズームレベルに応じて描画範囲を動的に調整します。

• 中心点の移動: ズームの中心をユーザーが指定できるようにすることで、特定の領域を詳細に観察することが可能になります。

これにより、興味のある部分を重点的に探索できます。

• 高精度計算: ズームレベルが高くなると、計算精度が重要になります。

高精度の数値演算ライブラリを使用することで、ズームイン時の精度を確保します。

他のフラクタル集合への応用

Mandelbrot集合の描画技術は、他のフラクタル集合にも応用可能です。

以下にいくつかの例を示します。

• Julia集合: Mandelbrot集合と密接に関連するJulia集合は、異なる初期条件で生成されるフラクタルです。

Mandelbrot集合の描画アルゴリズムを少し変更するだけで、Julia集合を描画できます。

• Burning Shipフラクタル: このフラクタルは、Mandelbrot集合の変種で、異なる反復関数を使用します。

Mandelbrot集合の描画技術を応用して、独特の形状を持つBurning Shipフラクタルを描画できます。

• Newtonフラクタル: 複素数平面上のニュートン法を用いて生成されるフラクタルで、Mandelbrot集合の描画技術を応用して、異なる数学的背景を持つフラクタルを描画できます。

これらの応用例を通じて、Mandelbrot集合の描画技術は多様なフラクタルの生成に活用でき、視覚的に魅力的な画像を作成することが可能です。

次のセクションでは、よくある質問について解説します。

よくある質問

まとめ

この記事では、Mandelbrot集合の定義や数学的背景、描画アルゴリズム、そして最適化技術と応用例について詳しく解説しました。

Mandelbrot集合の美しさと複雑さは、数学的な興味を引くだけでなく、視覚的な魅力も持ち合わせています。

これを機に、Mandelbrot集合の描画に挑戦し、さらなるフラクタルの世界を探求してみてはいかがでしょうか。