[C言語] Koch曲線の描画方法とアルゴリズムの実装
Koch曲線は、フラクタルの一種で、再帰的に直線を分割して生成されます。
描画方法は次の通りです。
まず、直線を3等分し、中央の部分を正三角形の一辺として外側に突き出すようにします。
この操作を再帰的に繰り返すことで、Koch曲線が形成されます。
C言語での実装では、再帰関数を用いて各ステップで直線を分割し、新しい点を計算して描画します。
再帰の深さを指定することで、曲線の複雑さを調整できます。
描画にはグラフィックスライブラリを使用することが一般的です。
Koch曲線とは
Koch曲線は、フラクタル図形の一種で、単純なルールに基づいて無限に複雑な形状を生成することができます。
このセクションでは、Koch曲線の基本的な概念とその歴史、特徴について説明します。
フラクタルの基本
フラクタルとは、自己相似性を持つ図形のことを指します。
自己相似性とは、図形の一部が全体と似た形状を持つ性質です。
フラクタルは、自然界の多くの現象をモデル化するために使用され、数学的には無限に細かい構造を持つことができます。
Koch曲線は、このフラクタルの一例であり、単純な生成ルールに従って複雑な形状を作り出します。
Koch曲線の歴史と背景
Koch曲線は、スウェーデンの数学者ヘルゲ・フォン・コッホによって1904年に発表されました。
彼は、直線を分割し、その一部を三角形の形に置き換えることで、無限に長い曲線を作り出す方法を示しました。
この曲線は、フラクタルの概念を理解する上で重要な役割を果たし、後に多くの数学者や科学者によって研究されることになりました。
Koch曲線の特徴
Koch曲線の特徴は、以下の通りです。
| 特徴 | 説明 |
|---|---|
| 自己相似性 | 曲線の一部が全体と同じ形状を持つ |
| 無限の長さ | 再帰的に生成されるため、理論上無限に長くなる |
| フラクタル次元 | 通常の直線よりも高い次元を持つ(約1.2619) |
Koch曲線は、単純なルールに基づいて生成されるにもかかわらず、非常に複雑で美しい形状を持つことが特徴です。
この特性により、数学的な興味だけでなく、芸術的な観点からも注目されています。
Koch曲線の数学的定義
Koch曲線は、単純な幾何学的ルールに基づいて生成されるフラクタル図形です。
このセクションでは、Koch曲線の初期形状と生成ルール、再帰的な生成プロセス、そしてフラクタル次元の計算について詳しく説明します。
初期形状と生成ルール
Koch曲線の生成は、以下の手順に従って行われます。
- 初期形状: Koch曲線の生成は、通常、直線から始まります。
この直線を「初期形状」と呼びます。
- 生成ルール: 初期形状を3等分し、中央の部分を取り除きます。
その代わりに、取り除いた部分に正三角形の2辺を追加します。
これにより、元の直線が4つの等しい長さの線分に置き換えられます。
この生成ルールを繰り返すことで、Koch曲線が形成されます。
再帰的な生成プロセス
Koch曲線は、再帰的なプロセスによって生成されます。
再帰的な生成プロセスは、以下のように進行します。
- ステップ1: 初期形状(直線)を3等分し、中央の部分を正三角形の2辺で置き換えます。
- ステップ2: 各線分に対して、同じ生成ルールを適用します。
- ステップ3: ステップ2を必要な回数だけ繰り返します。
このプロセスを繰り返すことで、Koch曲線は無限に複雑な形状を持つようになります。
フラクタル次元の計算
Koch曲線のフラクタル次元は、通常のユークリッド次元とは異なり、非整数の値を持ちます。
Koch曲線のフラクタル次元は、次の式で計算されます。
\[ D = \frac{\log(4)}{\log(3)} \approx 1.2619 \]
このフラクタル次元は、Koch曲線が通常の直線(次元1)よりも複雑であることを示しています。
フラクタル次元は、図形の複雑さや自己相似性を定量的に表現するための重要な指標です。
Koch曲線のようなフラクタルは、自然界の多くの現象をモデル化するために利用されることがあります。
C言語でのKoch曲線の実装
Koch曲線をC言語で実装するには、適切なライブラリを使用し、再帰的なアルゴリズムを設計する必要があります。
このセクションでは、Koch曲線を描画するための基本的な手順とアルゴリズムについて説明します。
必要なライブラリと環境設定
Koch曲線を描画するためには、グラフィックスライブラリが必要です。
ここでは、SDL(Simple DirectMedia Layer)を使用します。
SDLは、クロスプラットフォームのマルチメディアライブラリで、2Dグラフィックスの描画に適しています。
- SDLのインストール: SDLを使用するには、開発環境にSDLライブラリをインストールする必要があります。
Linuxでは、libsdl2-devパッケージをインストールすることで利用可能です。
- コンパイル設定: SDLを使用するために、コンパイル時に
-lSDL2オプションを指定します。
基本的なアルゴリズムの説明
Koch曲線の描画は、再帰的なアルゴリズムに基づいています。
基本的なアルゴリズムは以下の通りです。
- 初期化: 描画ウィンドウを作成し、初期の直線を設定します。
- 再帰描画: 再帰関数を使用して、Koch曲線を描画します。
- 終了処理: 描画が完了したら、ウィンドウを閉じてリソースを解放します。
再帰関数の設計
再帰関数は、Koch曲線の各セグメントを描画するために使用されます。
以下に、再帰関数の設計例を示します。
#include <SDL2/SDL.h>
#include <math.h>
// Koch曲線を描画する再帰関数
void drawKoch(SDL_Renderer *renderer, double x1, double y1, double x2, double y2, int depth) {
if (depth == 0) {
// 深さが0の場合、直線を描画
SDL_RenderDrawLine(renderer, x1, y1, x2, y2);
} else {
// 3等分点を計算
double dx = (x2 - x1) / 3.0;
double dy = (y2 - y1) / 3.0;
double x3 = x1 + dx;
double y3 = y1 + dy;
double x4 = x2 - dx;
double y4 = y2 - dy;
// 三角形の頂点を計算
double x5 = x3 + (dx - dy * sqrt(3)) / 2.0;
double y5 = y3 + (dy + dx * sqrt(3)) / 2.0;
// 再帰的に描画
drawKoch(renderer, x1, y1, x3, y3, depth - 1);
drawKoch(renderer, x3, y3, x5, y5, depth - 1);
drawKoch(renderer, x5, y5, x4, y4, depth - 1);
drawKoch(renderer, x4, y4, x2, y2, depth - 1);
}
}座標計算の方法
Koch曲線の座標計算は、直線を3等分し、中央の部分を正三角形の2辺で置き換えることで行います。
再帰関数内で、各セグメントの始点と終点を計算し、次の再帰呼び出しに渡します。
- 3等分点の計算: 各セグメントを3等分し、次のセグメントの始点と終点を計算します。
- 三角形の頂点の計算: 3等分点を基に、正三角形の頂点を計算します。
このようにして、Koch曲線の各セグメントを再帰的に描画することができます。
再帰の深さを増やすことで、より複雑なKoch曲線を生成することが可能です。
Koch曲線の描画
Koch曲線を描画するためには、適切なグラフィックスライブラリを選択し、座標変換や再帰的描画の実装を行う必要があります。
このセクションでは、SDLを使用したKoch曲線の描画方法について説明します。
グラフィックスライブラリの選択
Koch曲線の描画には、SDL(Simple DirectMedia Layer)を使用します。
SDLは、2Dグラフィックスの描画に適したクロスプラットフォームのライブラリで、簡単にウィンドウを作成し、描画を行うことができます。
描画のための座標変換
Koch曲線を描画する際には、ウィンドウの座標系に合わせて座標変換を行う必要があります。
通常、ウィンドウの左上が原点(0, 0)で、右下がウィンドウの幅と高さになります。
Koch曲線の描画範囲をウィンドウに収めるために、適切なスケーリングを行います。
再帰的描画の実装
再帰的描画は、Koch曲線の各セグメントを描画するために使用されます。
以下に、SDLを使用した再帰的描画の実装例を示します。
#include <SDL2/SDL.h>
#include <math.h>
void drawKoch(SDL_Renderer *renderer, double x1, double y1, double x2, double y2, int depth) {
if (depth == 0) {
SDL_RenderDrawLine(renderer, x1, y1, x2, y2);
} else {
double dx = (x2 - x1) / 3.0;
double dy = (y2 - y1) / 3.0;
double x3 = x1 + dx;
double y3 = y1 + dy;
double x4 = x2 - dx;
double y4 = y2 - dy;
double x5 = x3 + (dx - dy * sqrt(3)) / 2.0;
double y5 = y3 + (dy + dx * sqrt(3)) / 2.0;
drawKoch(renderer, x1, y1, x3, y3, depth - 1);
drawKoch(renderer, x3, y3, x5, y5, depth - 1);
drawKoch(renderer, x5, y5, x4, y4, depth - 1);
drawKoch(renderer, x4, y4, x2, y2, depth - 1);
}
}色とスタイルの設定
SDLでは、描画する線の色を設定することができます。
以下のコードでは、白色の線を設定しています。
SDL_SetRenderDrawColor(renderer, 255, 255, 255, 255); // 白色この設定を行うことで、Koch曲線を任意の色で描画することができます。
完成したプログラム
以下に、Koch曲線を描画するための完成したプログラムを示します。
#include <SDL2/SDL.h>
#include <math.h>
void drawKoch(SDL_Renderer *renderer, double x1, double y1, double x2, double y2, int depth);
int main(int argc, char *argv[]) {
SDL_Init(SDL_INIT_VIDEO);
SDL_Window *window = SDL_CreateWindow("Koch Curve", SDL_WINDOWPOS_UNDEFINED, SDL_WINDOWPOS_UNDEFINED, 800, 600, SDL_WINDOW_SHOWN);
SDL_Renderer *renderer = SDL_CreateRenderer(window, -1, SDL_RENDERER_ACCELERATED);
SDL_SetRenderDrawColor(renderer, 0, 0, 0, 255); // 背景色を黒に設定
SDL_RenderClear(renderer);
SDL_SetRenderDrawColor(renderer, 255, 255, 255, 255); // 線の色を白に設定
drawKoch(renderer, 100, 300, 700, 300, 5); // Koch曲線を描画
SDL_RenderPresent(renderer);
SDL_Delay(5000); // 5秒間表示
SDL_DestroyRenderer(renderer);
SDL_DestroyWindow(window);
SDL_Quit();
return 0;
}
void drawKoch(SDL_Renderer *renderer, double x1, double y1, double x2, double y2, int depth) {
if (depth == 0) {
SDL_RenderDrawLine(renderer, x1, y1, x2, y2);
} else {
double dx = (x2 - x1) / 3.0;
double dy = (y2 - y1) / 3.0;
double x3 = x1 + dx;
double y3 = y1 + dy;
double x4 = x2 - dx;
double y4 = y2 - dy;
double x5 = x3 + (dx - dy * sqrt(3)) / 2.0;
double y5 = y3 + (dy + dx * sqrt(3)) / 2.0;
drawKoch(renderer, x1, y1, x3, y3, depth - 1);
drawKoch(renderer, x3, y3, x5, y5, depth - 1);
drawKoch(renderer, x5, y5, x4, y4, depth - 1);
drawKoch(renderer, x4, y4, x2, y2, depth - 1);
}
}このプログラムは、SDLを使用してKoch曲線を描画します。
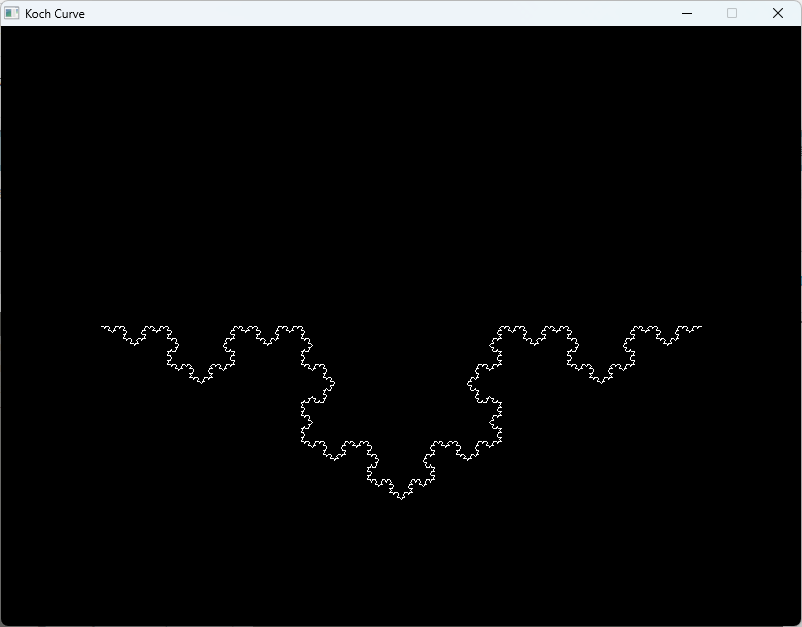
ウィンドウを作成し、再帰的にKoch曲線を描画した後、5秒間表示します。
描画の深さを変更することで、Koch曲線の複雑さを調整することができます。
応用例
Koch曲線は、その美しい形状と数学的特性から、さまざまな応用が考えられます。
このセクションでは、Koch曲線の応用例として、3Dフラクタルへの拡張、アニメーション化の手法、他のフラクタルとの組み合わせ、そして科学教育への応用について説明します。
3Dフラクタルへの拡張
Koch曲線は2次元のフラクタルですが、3次元に拡張することも可能です。
これにより、より複雑で興味深い形状を生成できます。
例えば、Koch曲線を3次元空間で展開し、Koch雪片やKoch立方体といった3Dフラクタルを作成することができます。
これらの3Dフラクタルは、コンピュータグラフィックスや建築デザインなどで利用されることがあります。
アニメーション化の手法
Koch曲線をアニメーション化することで、動的な視覚効果を得ることができます。
アニメーション化の手法としては、再帰の深さを時間とともに変化させる方法があります。
これにより、Koch曲線が徐々に複雑になっていく様子を視覚的に表現できます。
また、色や形状を時間とともに変化させることで、さらに豊かなアニメーションを作成することが可能です。
他のフラクタルとの組み合わせ
Koch曲線は、他のフラクタルと組み合わせることで、より複雑で美しい図形を生成することができます。
例えば、Mandelbrot集合やJulia集合と組み合わせることで、フラクタルアートを作成することができます。
これにより、数学的な美しさを視覚的に表現することが可能です。
科学教育への応用
Koch曲線は、数学やコンピュータサイエンスの教育においても有用です。
フラクタルの概念を理解するための教材として使用することで、学生に自己相似性や再帰の概念を直感的に理解させることができます。
また、プログラミング教育においても、Koch曲線の生成アルゴリズムを実装することで、再帰的思考やアルゴリズム設計のスキルを養うことができます。
これらの応用例を通じて、Koch曲線は単なる数学的な興味を超えて、さまざまな分野での実用的な価値を持つことが示されています。
まとめ
この記事では、Koch曲線の基本的な概念から数学的定義、C言語での実装方法、さらには応用例までを詳しく解説しました。
Koch曲線の持つフラクタルの特性やその美しさを、プログラミングを通じて具体的に体験することができるでしょう。
この記事を参考に、ぜひKoch曲線のプログラムを実際に作成し、その奥深い世界を探求してみてください。

![[C言語] ドラゴン曲線を計算するプログラムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44015.png)
![[C言語] トポロジカルソートを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44014.png)
![[C言語] ハノイの塔を解くプログラムの作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44019.png)
![[C言語] はさみうち法(非線形方程式)を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44017.png)
![[C言語] ナップザック問題を動的計画法で解く方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44016.png)
![[C言語] フラクタル圧縮を用いた画像圧縮方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44023.png)
![[C言語] プサイ関数/ポリガンマ関数を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44022.png)
![[C言語] フィボナッチ探索を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44021.png)
![[C言語] フィボナッチ数列を求めるアルゴリズムの書き方](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44020.png)
![[C言語] ベルマンフォード法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44029.png)
![[C言語] ベータ分布を計算して乱数を生成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44028.png)
![[C言語] ベータ関数を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44027.png)