[Python] 多変量正規分布を計算して可視化する
多変量正規分布は、複数の変数が正規分布に従う場合の分布を表します。
Pythonで多変量正規分布を計算し、可視化するには、NumPyとMatplotlib、SciPyなどのライブラリを使用します。
まず、NumPyを用いて平均ベクトルと共分散行列を定義し、SciPyのmultivariate_normal関数で分布を生成します。
次に、Matplotlibを使って2次元または3次元のプロットを作成し、分布の形状を視覚化します。
これにより、データの相関や分布の広がりを直感的に理解できます。
多変量正規分布とは
多変量正規分布は、統計学や機械学習において非常に重要な概念です。
これは、複数の変数が同時に正規分布に従う場合の分布を指します。
以下では、その基本的な概念と特性について詳しく説明します。
多変量正規分布の基本
多変量正規分布は、1つの変数ではなく、複数の変数が同時に正規分布に従う場合の分布です。
これにより、変数間の相関関係を考慮することができます。
多変量正規分布は、以下のように定義されます。
- 平均ベクトル: 各変数の平均値を含むベクトル。
- 共分散行列: 各変数間の共分散を含む行列。
これらの要素により、分布の形状や広がりが決まります。
平均ベクトルと共分散行列の役割
平均ベクトルと共分散行列は、多変量正規分布の中心的な役割を果たします。
- 平均ベクトル: 各変数の中心位置を示します。
例えば、2次元の場合、平均ベクトルは ([μ_1, μ_2]) のように表されます。
- 共分散行列: 変数間の相関を示します。
例えば、2次元の場合、共分散行列は以下のように表されます。
ここで、() と (
) は各変数の分散、(
) と (
) は変数間の共分散を示します。
多変量正規分布の特性
多変量正規分布にはいくつかの重要な特性があります。
- 対称性: 分布は平均ベクトルを中心に対称です。
- 楕円形の等高線: 2次元の場合、等高線は楕円形を形成します。
楕円の形状は共分散行列によって決まります。
- 独立性の条件: 共分散行列が対角行列である場合、変数は独立です。
これらの特性により、多変量正規分布はデータの相関関係を分析する際に非常に有用です。
Pythonでの多変量正規分布の計算
Pythonを使用して多変量正規分布を計算することは、データ分析や機械学習の分野で非常に役立ちます。
以下では、必要なライブラリのインストールから、実際に多変量正規分布を生成する方法までを説明します。
必要なライブラリのインストール
多変量正規分布を計算するためには、主にNumPyとSciPyという2つのライブラリを使用します。
これらのライブラリは、数値計算や統計処理において非常に強力です。
以下のコマンドを使用してインストールします。
pip install numpy scipyNumPyを使った平均ベクトルと共分散行列の定義
NumPyを使用して、平均ベクトルと共分散行列を定義します。
これらは多変量正規分布を生成するための基礎となります。
import numpy as np
# 平均ベクトルの定義
mean_vector = np.array([0, 0]) # 2次元の平均ベクトル
# 共分散行列の定義
covariance_matrix = np.array([[1, 0.5], [0.5, 1]]) # 2次元の共分散行列このコードでは、2次元の平均ベクトルと共分散行列を定義しています。
平均ベクトルは([0, 0])、共分散行列は()です。
SciPyを用いた多変量正規分布の生成
SciPyを使用して、多変量正規分布に従うデータを生成します。
SciPyのmultivariate_normal関数を利用します。
from scipy.stats import multivariate_normal
# 多変量正規分布の生成
distribution = multivariate_normal(mean=mean_vector, cov=covariance_matrix)
# サンプルデータの生成
sample_data = distribution.rvs(size=1000) # 1000個のサンプルを生成このコードでは、定義した平均ベクトルと共分散行列を使用して、多変量正規分布に従う1000個のサンプルデータを生成しています。
rvsメソッドを使用することで、指定した数のサンプルを簡単に取得できます。
これにより、Pythonを用いて多変量正規分布を計算し、サンプルデータを生成することができます。
生成したデータは、データ分析や機械学習の前処理として活用できます。
多変量正規分布の可視化
多変量正規分布を可視化することで、データの分布や相関関係を直感的に理解することができます。
以下では、PythonのMatplotlibライブラリを使用して、2次元および3次元のプロットを作成する方法を説明します。
Matplotlibによる2次元プロット
2次元の多変量正規分布を可視化するために、Matplotlibを使用します。
等高線プロットを作成することで、分布の形状を視覚的に確認できます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# 平均ベクトルと共分散行列の定義
mean_vector = np.array([0, 0])
covariance_matrix = np.array([[1, 0.5], [0.5, 1]])
# グリッドポイントの生成
x, y = np.mgrid[-3:3:.01, -3:3:.01]
pos = np.dstack((x, y))
# 多変量正規分布の生成
distribution = multivariate_normal(mean=mean_vector, cov=covariance_matrix)
# 等高線プロットの作成
plt.contourf(x, y, distribution.pdf(pos), cmap='viridis')
plt.title('2D Multivariate Normal Distribution')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.colorbar()
plt.show()このコードでは、2次元のグリッドポイントを生成し、contourf関数を使用して等高線プロットを作成しています。
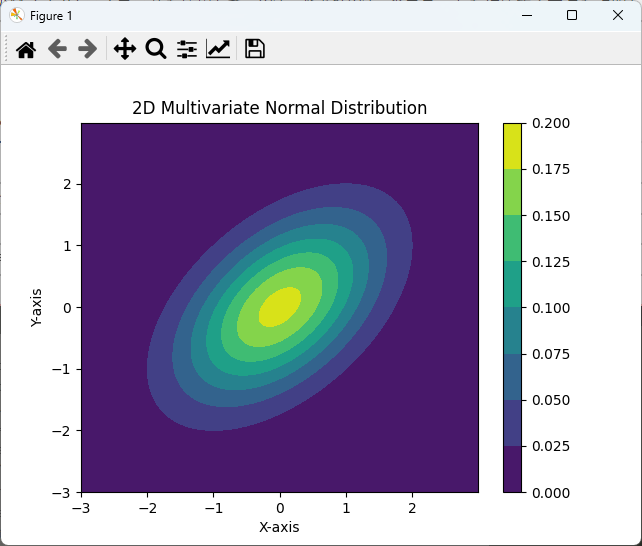
色の濃淡で分布の密度を表現しています。
3次元プロットの作成方法
3次元プロットを作成することで、より立体的に分布を理解することができます。
MatplotlibのAxes3Dを使用します。
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# 平均ベクトルと共分散行列の定義
mean_vector = np.array([0, 0])
covariance_matrix = np.array([[1, 0.5], [0.5, 1]])
# グリッドポイントの生成
x, y = np.mgrid[-3:3:.01, -3:3:.01]
pos = np.dstack((x, y))
# 多変量正規分布の生成
distribution = multivariate_normal(mean=mean_vector, cov=covariance_matrix)
# 3Dプロットの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# 多変量正規分布の確率密度関数を計算
z = distribution.pdf(pos)
# 3Dサーフェスプロットの作成
ax.plot_surface(x, y, z, cmap='viridis', edgecolor='none')
ax.set_title('3D Multivariate Normal Distribution')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Probability Density')
plt.show()このコードでは、plot_surface関数を使用して3次元のサーフェスプロットを作成しています。
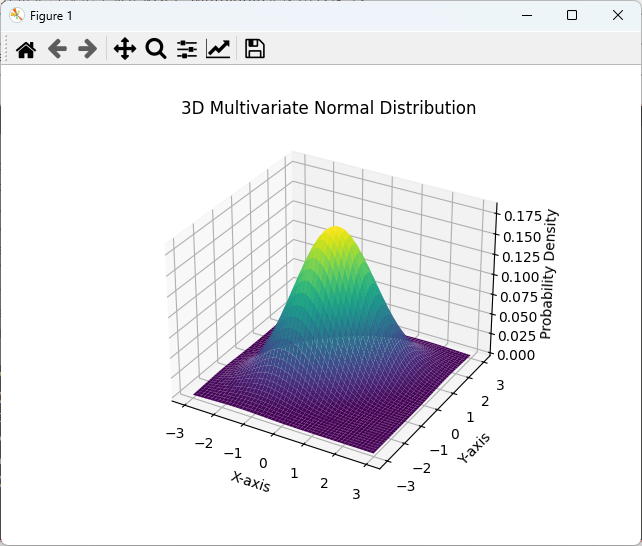
これにより、分布の高さ(密度)を視覚的に確認できます。
可視化のためのデータポイントの生成
可視化を行う際には、データポイントを生成してプロットに追加することも有効です。
以下のコードでは、生成したサンプルデータを2次元プロットに追加します。
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# 平均ベクトルと共分散行列の定義
mean_vector = np.array([0, 0])
covariance_matrix = np.array([[1, 0.5], [0.5, 1]])
# グリッドポイントの生成
x, y = np.mgrid[-3:3:.01, -3:3:.01]
pos = np.dstack((x, y))
# 多変量正規分布の生成
distribution = multivariate_normal(mean=mean_vector, cov=covariance_matrix)
# サンプルデータの生成
sample_data = distribution.rvs(size=100)
# サンプルデータのプロット
plt.scatter(sample_data[:, 0], sample_data[:, 1], c='red', marker='o', label='Sample Points')
plt.contourf(x, y, distribution.pdf(pos), cmap='viridis', alpha=0.5)
plt.title('2D Multivariate Normal Distribution with Samples')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.legend()
plt.show()このコードでは、赤い点でサンプルデータをプロットに追加し、分布の中での位置を視覚的に確認しています。
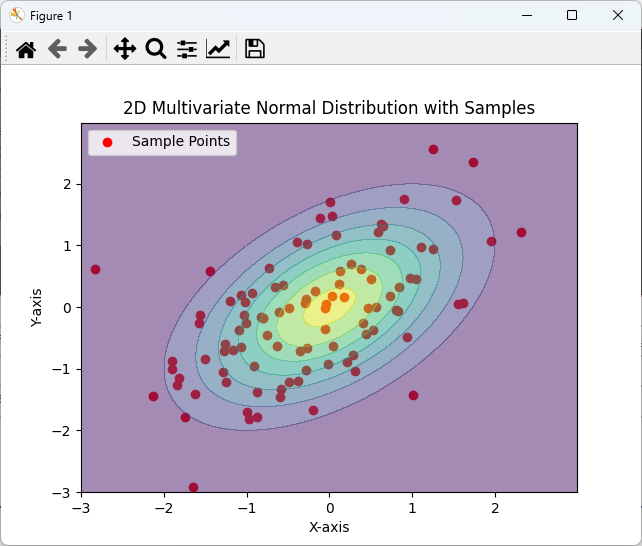
これにより、データの分布とサンプルの関係をより明確に理解できます。
応用例
多変量正規分布は、さまざまな分野で応用されています。
以下では、データの相関関係の分析、機械学習における特徴量の分布確認、シミュレーションデータの生成といった具体的な応用例を紹介します。
データの相関関係の分析
多変量正規分布は、データの相関関係を分析する際に非常に有用です。
共分散行列を用いることで、変数間の相関を定量的に評価できます。
- 共分散行列の解析: 共分散行列の非対角要素が大きい場合、変数間に強い相関があることを示します。
- 相関係数の計算: 共分散行列から相関係数を計算し、変数間の線形関係を評価します。
これにより、データセット内の変数がどの程度関連しているかを把握することができます。
機械学習における特徴量の分布確認
機械学習モデルの性能を向上させるためには、特徴量の分布を理解することが重要です。
多変量正規分布を用いることで、特徴量の分布を視覚化し、異常値や偏りを検出することができます。
- 特徴量の可視化: 多変量正規分布を用いて、特徴量の分布を2次元または3次元でプロットします。
- 異常値の検出: 分布から外れたデータポイントを特定し、異常値として扱います。
これにより、データの前処理や特徴量エンジニアリングの質を向上させることができます。
シミュレーションデータの生成
多変量正規分布は、シミュレーションデータの生成にも利用されます。
特に、現実のデータを模倣したデータセットを作成する際に役立ちます。
- データセットの拡張: 現実のデータに基づいて、多変量正規分布を用いて新たなデータポイントを生成します。
- モデルのテスト: シミュレーションデータを用いて、機械学習モデルの性能をテストします。
これにより、限られたデータセットを拡張し、モデルの汎化性能を評価することが可能になります。
まとめ
この記事では、多変量正規分布の基本からPythonを用いた計算方法、さらに可視化や応用例について詳しく解説しました。
多変量正規分布は、データの相関関係を分析したり、機械学習における特徴量の分布を確認したりする際に非常に有用です。
これを機に、実際のデータ分析や機械学習プロジェクトで多変量正規分布を活用し、データの理解を深める一助としてください。

![[Python] 便利な使い方を事例付きで紹介](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46950.png)

![[Python] turtleグラフィックスの使い方 – 入門レベルのグラフィック描画](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46960.png)
![[Python] sys.exit関数の使い方 – exit()との違いも解説](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46959.png)
![[Python] デバッガpdbの使い方 – ソースコードデバッグ](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46958.png)
![[Python] osモジュールの使い方 – OS関連処理の実装](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46957.png)
![[Python] namedtupleの使い方 – 名前付きフィールドを持つタプルの作成](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46956.png)
![[Python] help関数の使い方 – 関数やクラスのヘルプを表示](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46955.png)
![[Python] from importの使い方 – 特定の関数やクラスをインポートする](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46954.png)
![[Python] exit関数の使い方 – プログラムを途中で強制終了させる](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46953.png)
![[Python] Doxygenの使い方 – コードのドキュメント化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46952.png)
![[Python] dotenvの使い方 – 環境変数の取得/追加](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46951.png)