[Python] 2項分布を計算してグラフとして描画する方法
Pythonで2項分布を計算し、グラフとして描画するには、主にscipyとmatplotlibライブラリを使用します。
まず、scipy.statsのbinomクラスを用いて2項分布の確率質量関数(PMF)を計算します。
binom.pmf(k, n, p)を使って、試行回数n、成功確率p、成功回数kに対する確率を求めます。
次に、matplotlib.pyplotを用いて、計算した確率を棒グラフとして描画します。
plt.bar()を使ってx軸に成功回数、y軸に対応する確率を設定し、plt.show()でグラフを表示します。
これにより、2項分布の視覚的な理解が得られます。
2項分布とは
2項分布は、確率論と統計学における重要な概念で、特に離散確率分布の一種です。
これは、成功または失敗の2つの結果しかない試行を複数回行ったときに、成功する回数を表す分布です。
例えば、コインを10回投げたときに表が出る回数を考える場合などに用いられます。
2項分布の基本
2項分布は、以下の3つの要素によって定義されます。
| 要素 | 説明 |
|---|---|
| 試行回数 (n) | 試行を行う回数。例えば、コインを投げる回数。 |
| 成功確率 (p) | 各試行で成功する確率。例えば、コインの表が出る確率。 |
| 成功回数 (k) | 試行の中で成功する回数。 |
2項分布は、これらの要素を用いて、特定の成功回数が得られる確率を計算します。
2項分布の数学的定義
2項分布の確率質量関数 (PMF) は、以下の式で表されます。
[ P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} ]ここで、(\binom{n}{k}) は二項係数で、n回の試行の中でk回成功する組み合わせの数を表します。
この式を用いることで、特定の成功回数kが得られる確率を計算できます。
2項分布の応用例
2項分布は、さまざまな分野で応用されています。
以下にいくつかの例を示します。
- 品質管理: 製品の不良品率を評価する際に、一定数の製品を検査して不良品の数を数える。
- 医療試験: 新薬の効果を評価するために、治療が成功する患者の割合を調べる。
- マーケティング: 広告キャンペーンの効果を測定するために、広告を見た人の中で購入に至った人の割合を分析する。
これらの例では、2項分布を用いることで、特定の条件下での成功確率を統計的に評価することが可能です。
Pythonで2項分布を計算する方法
Pythonを用いて2項分布を計算するには、scipyライブラリを活用するのが一般的です。
このライブラリには、統計的な計算を行うための便利な関数が多数含まれています。
必要なライブラリのインストール
2項分布を計算するためには、scipyとnumpyライブラリが必要です。
これらのライブラリは、Pythonのパッケージ管理システムであるpipを使ってインストールできます。
pip install scipy numpyこのコマンドを実行することで、必要なライブラリがインストールされます。
scipy.statsのbinomクラスの使い方
scipy.statsモジュールには、2項分布を扱うためのbinomクラスが用意されています。
このクラスを使うことで、2項分布に関連するさまざまな計算を簡単に行うことができます。
from scipy.stats import binom
# 試行回数と成功確率を設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# binomオブジェクトを作成
binom_dist = binom(n, p)この例では、試行回数が10回、成功確率が0.5の2項分布を表すbinomオブジェクトを作成しています。
2項分布の確率質量関数(PMF)の計算
確率質量関数(PMF)は、特定の成功回数が得られる確率を計算するために使用されます。
binomクラスのpmfメソッドを使って計算できます。
# 成功回数kの確率を計算
k = 3 # 成功回数
probability = binom_dist.pmf(k)
print(f"成功回数{k}の確率: {probability}")このコードは、10回の試行で3回成功する確率を計算し、結果を出力します。
完成したプログラム
以下に、2項分布の計算を行う完全なプログラムを示します。
import numpy as np
from scipy.stats import binom
# 試行回数と成功確率を設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# binomオブジェクトを作成
binom_dist = binom(n, p)
# 各成功回数の確率を計算
for k in range(n + 1):
probability = binom_dist.pmf(k)
print(f"成功回数{k}の確率: {probability}")このプログラムは、0回から10回までの成功回数に対する確率を計算し、それぞれの結果を出力します。
これにより、2項分布の特性を視覚的に理解することができます。
2項分布をグラフとして描画する
2項分布の計算結果を視覚的に理解するためには、グラフとして描画することが有効です。
Pythonでは、matplotlibライブラリを使用して簡単にグラフを描画できます。
matplotlibの基本的な使い方
matplotlibは、Pythonでグラフを描画するための強力なライブラリです。
まずは、matplotlibをインストールし、基本的な使い方を確認しましょう。
pip install matplotlibインストール後、matplotlib.pyplotをインポートして使用します。
import matplotlib.pyplot as plt
# サンプルデータ
x = [1, 2, 3, 4, 5]
y = [1, 4, 9, 16, 25]
# グラフを描画
plt.plot(x, y)
plt.title("Sample Plot")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.show()このコードは、xとyのデータを用いて基本的な折れ線グラフを描画します。
2項分布のデータを準備する
2項分布のグラフを描画するためには、まず2項分布のデータを準備します。
scipy.statsのbinomクラスを使用して、各成功回数に対する確率を計算します。
import numpy as np
from scipy.stats import binom
# 試行回数と成功確率を設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# 各成功回数の確率を計算
k_values = np.arange(n + 1)
probabilities = binom.pmf(k_values, n, p)このコードは、0回から10回までの成功回数に対する確率を計算し、k_valuesとprobabilitiesに格納します。
棒グラフの描画方法
準備したデータを用いて、棒グラフを描画します。
matplotlibのbar関数を使用します。
import matplotlib.pyplot as plt
# 棒グラフを描画
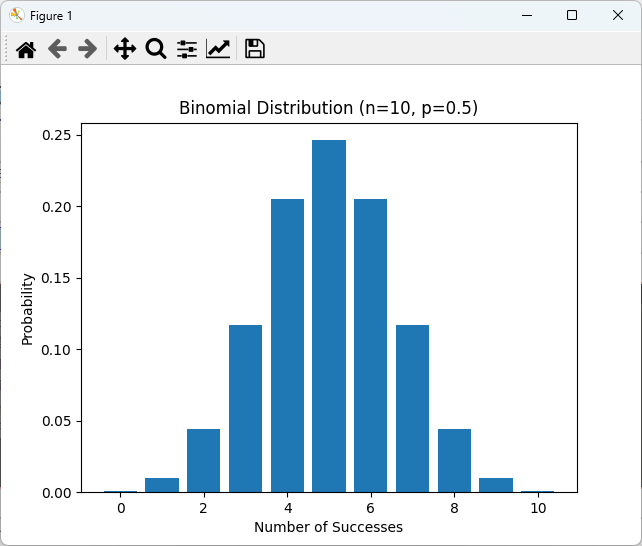
plt.bar(k_values, probabilities)
plt.title("Binomial Distribution (n=10, p=0.5)")
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.show()このコードは、2項分布の棒グラフを描画し、成功回数ごとの確率を視覚的に示します。
グラフのカスタマイズ
描画したグラフをカスタマイズすることで、より見やすくすることができます。
例えば、色やラベルを変更することが可能です。
# カスタマイズされた棒グラフを描画
plt.bar(k_values, probabilities, color='skyblue', edgecolor='black')
plt.title("Binomial Distribution (n=10, p=0.5)")
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.xticks(k_values) # x軸の目盛りを設定
plt.grid(axis='y', linestyle='--', alpha=0.7) # y軸にグリッドを追加
plt.show()このコードでは、棒の色をskyblueに設定し、x軸の目盛りを明示的に設定しています。
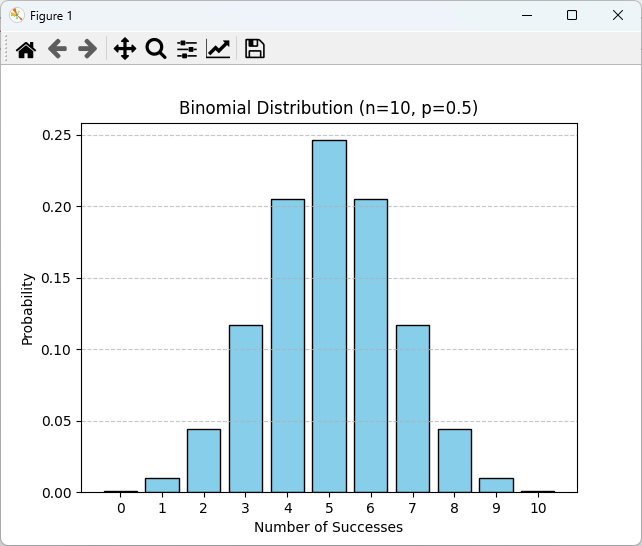
また、y軸にグリッドを追加することで、グラフの読みやすさを向上させています。
応用例
2項分布は、さまざまな応用が可能です。
ここでは、累積分布関数の計算と描画、シミュレーション、統計的検定への応用について説明します。
2項分布の累積分布関数(CDF)の計算と描画
累積分布関数(CDF)は、特定の成功回数以下の確率を計算するために使用されます。
scipy.statsのbinomクラスのcdfメソッドを使って計算できます。
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
# 試行回数と成功確率を設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# 各成功回数の累積確率を計算
k_values = np.arange(n + 1)
cumulative_probabilities = binom.cdf(k_values, n, p)
# 累積分布関数を描画
plt.step(k_values, cumulative_probabilities, where='mid', color='orange')
plt.title("Cumulative Distribution Function (CDF)")
plt.xlabel("Number of Successes")
plt.ylabel("Cumulative Probability")
plt.grid(True)
plt.show()このコードは、2項分布の累積分布関数を計算し、ステッププロットとして描画します。
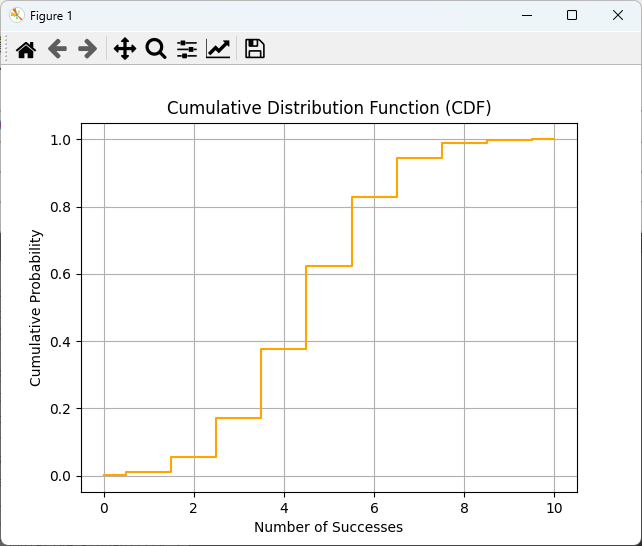
これにより、特定の成功回数以下の確率を視覚的に確認できます。
2項分布のシミュレーション
2項分布のシミュレーションを行うことで、実際の試行を模擬することができます。
numpyのrandom.binomial関数を使用して、シミュレーションを行います。
import numpy as np
# 試行回数と成功確率を設定
n = 10 # 試行回数
p = 0.5 # 成功確率
num_simulations = 1000 # シミュレーション回数
# 2項分布のシミュレーション
simulated_data = np.random.binomial(n, p, num_simulations)
# シミュレーション結果のヒストグラムを描画
plt.hist(simulated_data, bins=np.arange(n + 2) - 0.5, density=True, color='lightgreen', edgecolor='black')
plt.title("Binomial Distribution Simulation")
plt.xlabel("Number of Successes")
plt.ylabel("Frequency")
plt.grid(True)
plt.show()このコードは、1000回のシミュレーションを行い、その結果をヒストグラムとして描画します。
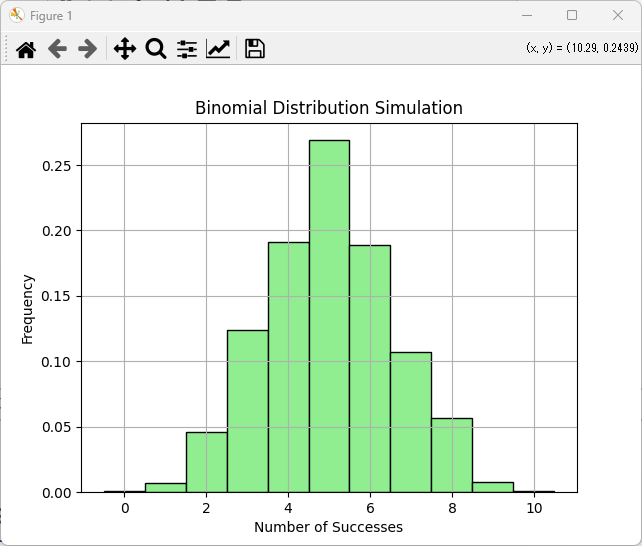
これにより、2項分布の特性を実験的に確認できます。
2項分布を用いた統計的検定
2項分布は、統計的検定にも利用されます。
例えば、ある製品の不良率が特定の値と異なるかどうかを検定する場合に使用されます。
ここでは、片側検定の例を示します。
from scipy.stats import binom_test
# 実際の成功回数と試行回数
observed_successes = 7
n = 10
p = 0.5 # 帰無仮説の成功確率
# 片側検定を実行
p_value = binom_test(observed_successes, n, p, alternative='greater')
print(f"p-value: {p_value}")このコードは、10回の試行で7回成功した場合に、成功確率が0.5よりも大きいかどうかを検定します。
p-valueが小さい場合、帰無仮説を棄却し、成功確率が0.5よりも大きいと結論付けることができます。
まとめ
この記事では、Pythonを用いて2項分布を計算し、グラフとして描画する方法について詳しく解説しました。
2項分布の基本から始まり、scipyライブラリを使った計算方法、matplotlibを用いたグラフの描画、さらには応用例として累積分布関数の計算やシミュレーション、統計的検定についても触れました。
これらの知識を活用することで、データ分析や統計的な問題に対してより深い洞察を得ることができるでしょう。
ぜひ、実際のデータに対してこれらの手法を試し、さらなる分析に挑戦してみてください。

![[Python] deapライブラリの使い方 – 遺伝的アルゴリズム](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46601.png)
![[Python] bisectライブラリの使い方 – ニ分探索の効率化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46600.png)
![[Python] a*(A Star)探索アルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43234.png)
![[Python] ベジェ曲線を実装する方法(二次ベジェ/三次ベジェ)](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43239.png)
![[Python] ベッセル関数を使ったグラフ作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43238.png)
![[Python] ベルヌーイ分布を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43237.png)
![[Python] エイトケンのΔ2乗加速法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43236.png)
![[Python] アッカーマン関数のプログラムを作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43235.png)
![[Python] matplotlibでC曲線を描画する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43245.png)
![[Python] CRC(巡回冗長検査)のアルゴリズムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-43244.png)