[Python/Numpy] meshgrid関数の使い方 – リストから格子列を生成する
meshgrid関数は、1次元配列(リスト)を入力として、格子状の座標データを生成するために使用されます。
主に2Dや3Dのグリッドを作成する際に便利です。
例えば、2つの1次元配列を渡すと、それらを基にした2Dグリッドの座標を表す2つの2D配列を返します。
引数indexingで’xy'(デフォルト)または’ij’を指定して、生成される配列の順序を制御できます。
meshgrid関数とは
meshgrid関数は、NumPyライブラリに含まれる非常に便利な関数で、2次元の格子点を生成するために使用されます。
特に、数値計算やデータ可視化の際に、2つの1次元配列から2次元の座標行列を作成するのに役立ちます。
これにより、関数の評価やグラフの描画が容易になります。
例えば、x軸とy軸の値を持つ2つの配列があるとき、meshgridを使うことで、各点の組み合わせを表す2次元の配列を生成できます。
これにより、数値解析やグラフ作成の際に、座標を簡単に扱うことが可能になります。
以下は、meshgrid関数の基本的な使い方の例です。
meshgrid関数の基本的な使い方
meshgrid関数は、2つの1次元配列を入力として受け取り、それぞれの配列の要素の組み合わせから2次元の格子点を生成します。
基本的な使い方は以下の通りです。
基本的な構文
import numpy as np
x = np.array([1, 2, 3])
y = np.array([4, 5])
X, Y = np.meshgrid(x, y)import numpy as np: NumPyライブラリをインポートします。xとy: 1次元の配列を定義します。np.meshgrid(x, y):xとyの要素の組み合わせから2次元の配列XとYを生成します。
上記のコードを実行すると、以下のような出力が得られます。
X:
[[1 2 3]
[1 2 3]]
Y:
[[4 4 4]
[5 5 5]]出力の解説
Xは、xの各要素が行として繰り返され、Yは、yの各要素が列として繰り返される形で生成されます。- これにより、各点の座標を簡単に扱うことができ、数値計算やグラフ描画に利用できます。
meshgrid関数の引数とオプション
meshgrid関数は、主に2つの引数を受け取りますが、オプションとしていくつかのパラメータも指定できます。
以下に、主要な引数とオプションを説明します。
引数
| 引数名 | 説明 |
|---|---|
x | 1次元配列。x軸の座標を指定します。 |
y | 1次元配列。y軸の座標を指定します。 |
オプション
| オプション名 | 説明 |
|---|---|
sparse | Trueを指定すると、スパース行列形式で出力されます。デフォルトはFalseです。 |
indexing | ‘xy’または‘ij’を指定できます。デフォルトは‘xy’で、行列のインデックスをx-y形式で生成します。‘ij’を指定すると、行列のインデックスをi-j形式で生成します。 |
以下は、sparseオプションを使用した例です。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([4, 5])
X, Y = np.meshgrid(x, y, sparse=True)X:
[[1 2 3]]
Y:
[[4]
[5]]sparse=Trueを指定すると、出力される配列はスパース形式になり、メモリの使用量が削減されます。indexingオプションを使うことで、生成される配列のインデックス形式を変更でき、特定の用途に応じた格子点の生成が可能になります。
実践例:meshgrid関数を使った具体的なコード例
ここでは、meshgrid関数を使用して、2次元の関数を評価し、その結果を可視化する具体的なコード例を示します。
この例では、2次元のガウス関数を計算し、その結果をヒートマップとして表示します。
コード例
import numpy as np
import matplotlib.pyplot as plt
# x軸とy軸の範囲を設定
x = np.linspace(-5, 5, 100) # -5から5までの100点
y = np.linspace(-5, 5, 100) # -5から5までの100点
# meshgridを使用して格子点を生成
X, Y = np.meshgrid(x, y)
# 2次元ガウス関数の定義
Z = np.exp(-(X**2 + Y**2))
# ヒートマップの表示
plt.imshow(Z, extent=(-5, 5, -5, 5), origin='lower', cmap='viridis')
plt.colorbar(label='関数の値')
plt.title('2次元ガウス関数のヒートマップ')
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.show()上記のコードを実行すると、以下のようなヒートマップが表示されます。
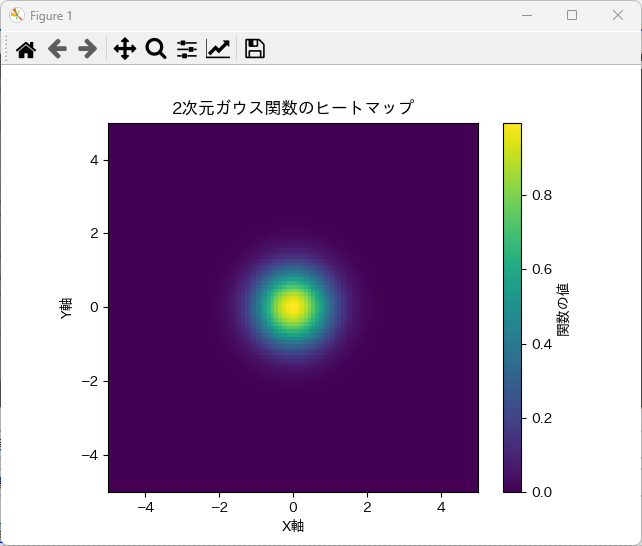
np.linspaceを使用して、-5から5までの範囲で100点の配列を生成します。meshgridを使って、x軸とy軸の格子点を生成し、2次元ガウス関数を計算します。plt.imshowを使用して、計算した関数の値をヒートマップとして可視化します。- このように、
meshgrid関数を利用することで、2次元のデータを簡単に扱い、視覚的に表現することができます。
meshgrid関数の応用テクニック
meshgrid関数は、基本的な格子点の生成だけでなく、さまざまな応用が可能です。
以下に、いくつかの応用テクニックを紹介します。
3次元プロットの生成
meshgridを使用して3次元のデータを生成し、3Dプロットを作成することができます。
以下はその例です。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# x軸とy軸の範囲を設定
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
# meshgridを使用して格子点を生成
X, Y = np.meshgrid(x, y)
# 3次元の関数を定義
Z = np.sin(np.sqrt(X**2 + Y**2))
# 3Dプロットの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_title('3次元のサイン関数')
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')
plt.show()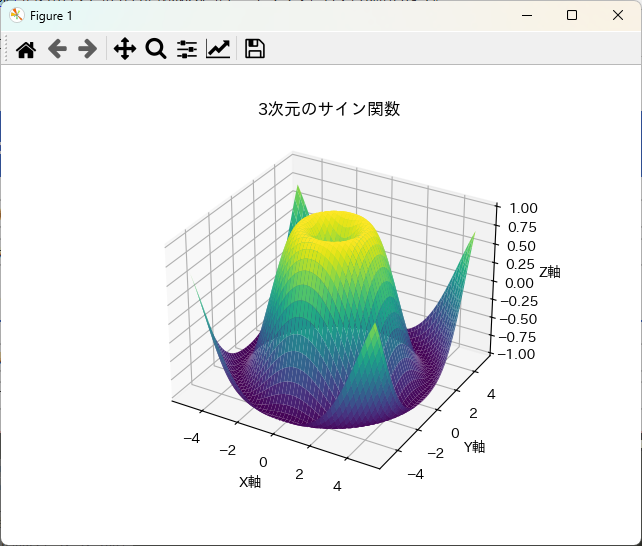
複数の関数の同時評価
meshgridを使って、複数の関数を同時に評価し、比較することができます。
以下は、2つの異なる関数を同時にプロットする例です。
import numpy as np
import matplotlib.pyplot as plt
# x軸とy軸の範囲を設定
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
# meshgridを使用して格子点を生成
X, Y = np.meshgrid(x, y)
# 2つの異なる関数を定義
Z1 = np.sin(np.sqrt(X**2 + Y**2))
Z2 = np.cos(np.sqrt(X**2 + Y**2))
# プロット
plt.contourf(X, Y, Z1, alpha=0.5, cmap='Blues')
plt.contourf(X, Y, Z2, alpha=0.5, cmap='Reds')
plt.title('2つの関数の同時評価')
plt.xlabel('X軸')
plt.ylabel('Y軸')
plt.colorbar(label='関数の値')
plt.show()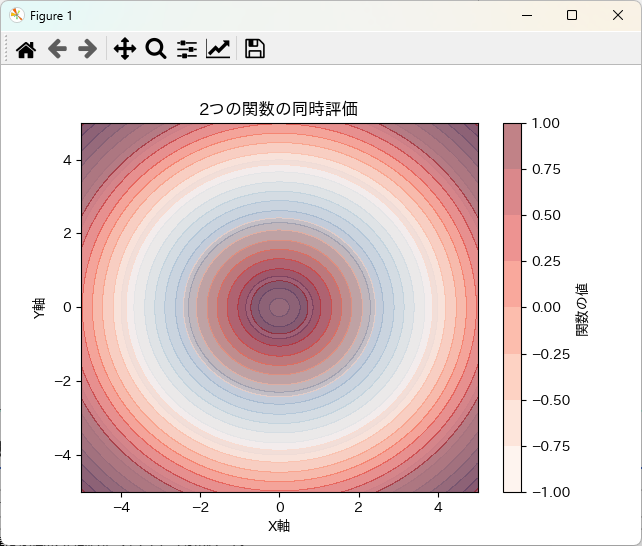
スパース行列の利用
meshgridのsparseオプションを利用することで、大規模なデータセットを扱う際にメモリの使用量を削減できます。
以下はその例です。
import numpy as np
# x軸とy軸の範囲を設定
x = np.linspace(0, 10, 1000)
y = np.linspace(0, 10, 1000)
# meshgridを使用してスパース行列を生成
X, Y = np.meshgrid(x, y, sparse=True)
# スパース行列の形状を確認
print("Xの形状:", X.shape)
print("Yの形状:", Y.shape)- 3次元プロットでは、
mpl_toolkits.mplot3dを使用して、3Dグラフを描画できます。 - 複数の関数を同時に評価することで、異なる関数の挙動を視覚的に比較できます。
- スパース行列を利用することで、大規模なデータを効率的に扱うことができ、計算資源を節約できます。
これらのテクニックを活用することで、meshgrid関数の可能性を広げることができます。
よくあるエラーとその対処法
meshgrid関数を使用する際に遭遇する可能性のある一般的なエラーと、その対処法について説明します。
これにより、スムーズにプログラミングを進めることができます。
引数の形状が一致しないエラー
エラーメッセージ
ValueError: shapes (n,) and (m,) not aligned: 1D arrays must be of the same length原因
meshgrid関数に渡す1次元配列の形状が一致しない場合に発生します。
例えば、異なる長さの配列を渡すとこのエラーが発生します。
対処法
引数として渡す配列の形状を確認し、同じ長さの配列を使用するように修正します。
import numpy as np
# 正しい形状の配列を使用
x = np.array([1, 2, 3])
y = np.array([4, 5, 6]) # 同じ長さの配列
X, Y = np.meshgrid(x, y)スパース行列の使用時の誤解
エラーメッセージ
TypeError: meshgrid() got an unexpected keyword argument 'sparse'原因
NumPyのバージョンが古い場合、sparseオプションがサポートされていないことがあります。
対処法
NumPyを最新バージョンにアップデートします。
以下のコマンドを使用してアップデートできます。
pip install --upgrade numpy不適切なインデックス形式の指定
エラーメッセージ
ValueError: invalid indexing method: 'invalid_indexing'原因
indexingオプションに無効な値を指定した場合に発生します。
'xy'または'ij'以外の値を指定するとこのエラーが出ます。
対処法
indexingオプションには、正しい値'xy'または'ij'を指定するように修正します。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
X, Y = np.meshgrid(x, y, indexing='ij') # 正しい指定メモリ不足エラー
エラーメッセージ
MemoryError: Unable to allocate array with shape (n, m) and data type float64原因
非常に大きな配列を生成しようとした場合、メモリが不足することがあります。
対処法
生成する配列のサイズを小さくするか、スパース行列を使用してメモリの使用量を削減します。
import numpy as np
# 小さな範囲で配列を生成
x = np.linspace(-1, 1, 100) # サイズを小さくする
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)これらのエラーは、meshgrid関数を使用する際によく発生するものです。
エラーメッセージを注意深く読み、原因を特定することで、適切な対処法を講じることができます。
正しい引数の形状やオプションの指定を行うことで、スムーズにプログラミングを進めることができるでしょう。
meshgrid関数の代替手法と比較
meshgrid関数は非常に便利ですが、他にも格子点を生成するための手法があります。
ここでは、meshgridの代替手法とその比較を行います。
numpy.indices関数
numpy.indices関数は、指定した形状のインデックス配列を生成します。
これにより、格子点を生成することができます。
import numpy as np
# 3x3の格子点を生成
indices = np.indices((3, 3))
print(indices)[[[0 0 0]
[1 1 1]
[2 2 2]]
[[0 1 2]
[0 1 2]
[0 1 2]]]numpy.mgrid関数
numpy.mgridは、メッシュグリッドを生成するためのもう一つの方法です。
スライスオブジェクトを使用して、範囲を指定します。
import numpy as np
# -5から5までの範囲で格子点を生成
X, Y = np.mgrid[-5:5:100j, -5:5:100j]
print(X.shape, Y.shape)(100, 100) (100, 100)numpy.meshgridとの比較
| 特徴 | meshgrid | numpy.indices | numpy.mgrid |
|---|---|---|---|
| 引数の形式 | 1次元配列 | 形状をタプルで指定 | スライスオブジェクトを使用 |
| 出力形式 | 2次元配列 | 3次元配列 | 2次元配列 |
| メモリ効率 | 通常 | 大きな配列の場合は高い | 通常 |
| 使用の簡便さ | 簡単 | やや複雑 | 簡単 |
どの手法を選ぶべきか
meshgrid: 最も一般的で、直感的に使いやすい。
2次元の格子点を生成する際に広く使用される。
numpy.indices: インデックスを生成する必要がある場合に便利。
特に、配列のインデックスを直接扱いたい場合に適している。
numpy.mgrid: スライスを使って範囲を指定できるため、特定の範囲での格子点を生成するのに便利。
大きな配列を生成する際には、メモリ効率が良い場合もある。
これらの代替手法は、それぞれ異なる特徴を持っています。
使用する場面や目的に応じて、最適な手法を選択することが重要です。
meshgridは一般的な用途に適していますが、特定の要件に応じて他の手法を検討することも有益です。
まとめ
この記事では、PythonのNumPyライブラリにおけるmeshgrid関数の基本的な使い方や、引数、オプション、実践例、応用テクニック、よくあるエラーとその対処法、さらには代替手法との比較について詳しく解説しました。
これにより、meshgrid関数を効果的に活用するための知識が得られたことでしょう。
今後は、実際のデータ解析や可視化のプロジェクトにおいて、これらのテクニックを積極的に活用してみてください。

![[Python] reshape関数の使い方 – ndarrayの形状を変換する](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46875.png)
![[Python] np.zerosの使い方 – 0で初期化された配列(リスト)を作成する](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46874.png)
![[Python/NumPy] np.arangeの使い方 – 連番/等差数列の作成](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46873.png)
![[Python] NumPyで1次元配列を作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-41250.png)

![[Python] NumPyで2次元配列を作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-41251.png)
![[Python] NumPy – 2次元配列の対角線要素を取得する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-41252.png)
![[Python] NumPy – 行列を作成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-41258.png)
![[Python] NumPy – np.ndarrayの使い方](https://af-e.net/wp-content/uploads/2024/10/thumbnail-41253.png)
![[Python] NumPyをインストールする方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-41254.png)