[Python] networkXの使い方 – ネットワーク図の作成・可視化・分析
NetworkXはPythonでネットワーク(グラフ)を作成・可視化・分析するためのライブラリです。
ノード(点)とエッジ(線)を定義してグラフを構築できます。
グラフには無向グラフ、有向グラフ、重み付きグラフなどが含まれます。
add_nodeやadd_edgeでノードやエッジを追加し、draw関数で可視化が可能です。
さらに、ネットワークの中心性、クラスタリング係数、最短経路などの分析も簡単に行えます。
NetworkXとは何か
NetworkXは、Pythonで書かれた強力なライブラリで、複雑なネットワークやグラフの作成、操作、分析を行うためのツールです。
特に、ソーシャルネットワーク、交通網、通信網など、さまざまな分野でのネットワークデータの可視化や解析に利用されています。
以下に、NetworkXの主な特徴を示します。
| 特徴 | 説明 |
|---|---|
| グラフの作成 | ノード(点)とエッジ(線)を簡単に作成可能 |
| 可視化 | MatplotlibやGraphvizと連携して可視化が可能 |
| アルゴリズム | 最短経路、クラスタリング、中心性などの分析機能を提供 |
| 拡張性 | 他のライブラリとの統合が容易 |
NetworkXを使用することで、複雑なネットワークの構造を理解しやすくし、データ分析を効率的に行うことができます。
NetworkXでのネットワーク図の基本操作
NetworkXを使用してネットワーク図を作成するための基本的な操作を紹介します。
以下の手順で、ノードとエッジを追加し、簡単なネットワーク図を作成することができます。
ライブラリのインポート
まず、NetworkXとMatplotlibをインポートします。
Matplotlibは、ネットワーク図を可視化するために使用します。
import networkx as nx
import matplotlib.pyplot as pltグラフの作成
次に、空のグラフを作成します。
NetworkXでは、無向グラフや有向グラフを作成することができます。
ここでは無向グラフを作成します。
# 無向グラフの作成
G = nx.Graph()ノードの追加
ノードを追加するには、add_nodeメソッドを使用します。
以下の例では、3つのノードを追加します。
# ノードの追加
G.add_node("A")
G.add_node("B")
G.add_node("C")エッジの追加
エッジを追加するには、add_edgeメソッドを使用します。
ノード間の接続を定義します。
# エッジの追加
G.add_edge("A", "B")
G.add_edge("B", "C")
G.add_edge("C", "A")ネットワーク図の描画
最後に、作成したネットワーク図を描画します。
drawメソッドを使用して、グラフを可視化します。
# ネットワーク図の描画
nx.draw(G, with_labels=True, node_color='lightblue', node_size=2000, font_size=16, font_color='black')
plt.show()上記のコードを実行すると、以下のようなネットワーク図が表示されます。
A -- B
| |
C ----このようにして、NetworkXを使って基本的なネットワーク図を作成することができます。
ノードやエッジを追加することで、より複雑なネットワークを構築することも可能です。
NetworkXを使ったネットワーク図の可視化
NetworkXを使用すると、作成したネットワーク図を簡単に可視化できます。
可視化は、ネットワークの構造や関係性を理解するために非常に重要です。
ここでは、基本的な可視化方法とカスタマイズのテクニックを紹介します。
基本的な可視化
まずは、基本的なネットワーク図の描画方法を見ていきます。
以下のコードでは、ノードとエッジを持つグラフを作成し、可視化します。
import networkx as nx
import matplotlib.pyplot as plt
# グラフの作成
G = nx.Graph()
G.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C")])
# ネットワーク図の描画
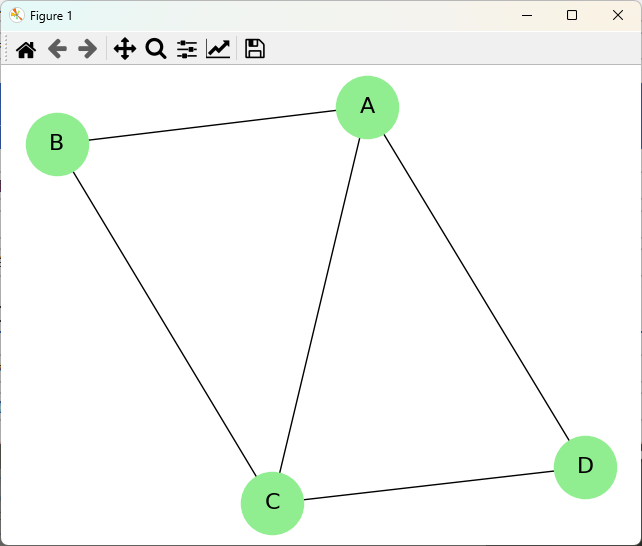
nx.draw(G, with_labels=True, node_color='lightgreen', node_size=2000, font_size=16, font_color='black')
plt.title("基本的なネットワーク図")
plt.show()このコードを実行すると、以下のような基本的なネットワーク図が表示されます。
ノードの色とサイズのカスタマイズ
ノードの色やサイズを変更することで、ネットワーク図をより視覚的にわかりやすくすることができます。
以下の例では、ノードのサイズをノードの次数に基づいて変更します。
# ノードのサイズを次数に基づいて設定
node_sizes = [G.degree(n) * 500 for n in G.nodes()]
# ネットワーク図の描画
nx.draw(G, with_labels=True, node_color='lightblue', node_size=node_sizes, font_size=16, font_color='black')
plt.title("ノードのサイズを次数に基づいて変更")
plt.show()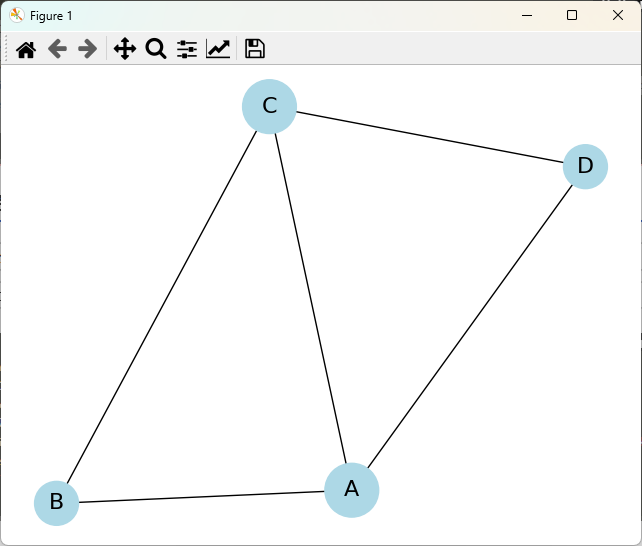
エッジの色とスタイルのカスタマイズ
エッジの色やスタイルもカスタマイズ可能です。
以下の例では、エッジの色をランダムに設定します。
import random
# エッジの色をランダムに設定
edge_colors = [random.choice(['red', 'blue', 'green', 'orange']) for _ in G.edges()]
# ネットワーク図の描画
nx.draw(G, with_labels=True, node_color='lightyellow', node_size=2000, font_size=16, font_color='black', edge_color=edge_colors)
plt.title("エッジの色をランダムに設定")
plt.show()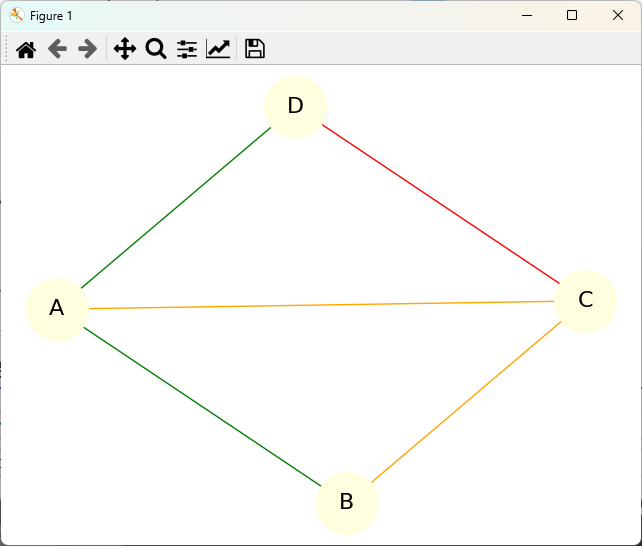
レイアウトの変更
NetworkXでは、さまざまなレイアウトを使用してネットワーク図を描画できます。
以下の例では、spring_layoutを使用して、ノードの位置を自動的に調整します。
# レイアウトの変更
pos = nx.spring_layout(G)
# ネットワーク図の描画
nx.draw(G, pos, with_labels=True, node_color='lightcoral', node_size=2000, font_size=16, font_color='black')
plt.title("スプリングレイアウトを使用したネットワーク図")
plt.show()これらの方法を使うことで、NetworkXを利用したネットワーク図の可視化をより効果的に行うことができます。
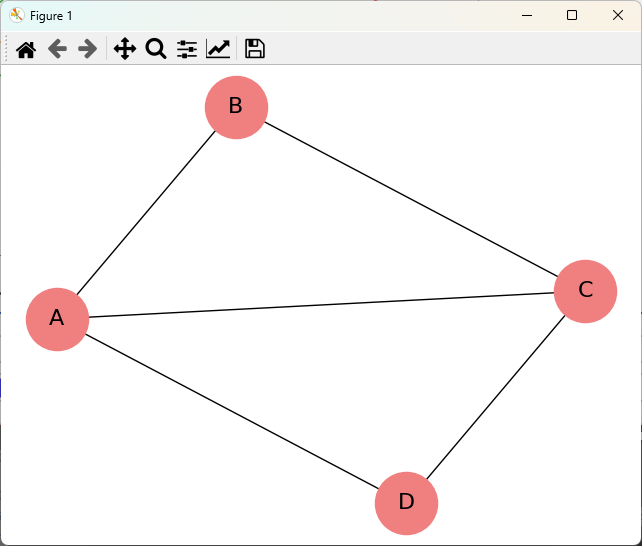
可視化は、データの理解を深めるための重要な手段ですので、さまざまなカスタマイズを試してみてください。
NetworkXを使ったネットワーク分析
NetworkXは、ネットワークの構造や特性を分析するための多くの機能を提供しています。
ここでは、基本的なネットワーク分析の手法をいくつか紹介します。
具体的には、ノードの次数、最短経路、中心性の計算について説明します。
ノードの次数
ノードの次数は、そのノードに接続されているエッジの数を示します。
次数は、ネットワーク内のノードの重要性を理解するための基本的な指標です。
以下のコードでは、各ノードの次数を計算し、表示します。
import networkx as nx
# グラフの作成
G = nx.Graph()
G.add_edges_from([("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C")])
# 各ノードの次数を計算
degree_dict = dict(G.degree())
# 結果の表示
print("各ノードの次数:")
for node, degree in degree_dict.items():
print(f"ノード {node}: {degree}")出力結果は以下のようになります。
各ノードの次数:
ノード A: 3
ノード B: 2
ノード C: 3
ノード D: 2最短経路の計算
最短経路は、2つのノード間の最小エッジ数を示します。
NetworkXでは、shortest_pathメソッドを使用して最短経路を計算できます。
以下の例では、ノードAからノードDまでの最短経路を求めます。
# ノードAからノードDまでの最短経路を計算
shortest_path = nx.shortest_path(G, source="A", target="D")
# 結果の表示
print("ノードAからノードDまでの最短経路:", shortest_path)出力結果は以下のようになります。
ノードAからノードDまでの最短経路: ['A', 'D']中心性の計算
中心性は、ネットワーク内のノードの重要性を示す指標です。
NetworkXでは、さまざまな中心性の指標を計算できますが、ここでは次数中心性とベットウィーンネス中心性を紹介します。
1. 次数中心性
次数中心性は、ノードの次数を基にした指標です。
以下のコードで計算できます。
# 次数中心性の計算
degree_centrality = nx.degree_centrality(G)
# 結果の表示
print("次数中心性:")
for node, centrality in degree_centrality.items():
print(f"ノード {node}: {centrality:.2f}")出力結果は以下のようになります。
次数中心性:
ノード A: 0.75
ノード B: 0.50
ノード C: 0.75
ノード D: 0.502. ベットウィーンネス中心性
ベットウィーンネス中心性は、他のノード間の最短経路におけるノードの重要性を示します。
以下のコードで計算できます。
# ベットウィーンネス中心性の計算
betweenness_centrality = nx.betweenness_centrality(G)
# 結果の表示
print("ベットウィーンネス中心性:")
for node, centrality in betweenness_centrality.items():
print(f"ノード {node}: {centrality:.2f}")出力結果は以下のようになります。
ベットウィーンネス中心性:
ノード A: 0.00
ノード B: 0.25
ノード C: 0.25
ノード D: 0.00NetworkXを使用することで、ネットワークの基本的な分析を簡単に行うことができます。
ノードの次数、最短経路、中心性の計算は、ネットワークの構造や特性を理解するための重要な手法です。
これらの分析を通じて、ネットワークの特性を深く理解し、さまざまな応用に活かすことができます。
応用例:実際のデータを使ったネットワーク分析
ここでは、実際のデータを使用してNetworkXを用いたネットワーク分析の応用例を紹介します。
具体的には、ソーシャルネットワークデータを用いて、ノードの中心性や最短経路を分析します。
サンプルデータとして、友人関係を示すエッジリストを使用します。
データの準備
まず、友人関係を示すエッジリストを作成します。
このデータは、ノード(ユーザー)間の関係を示しています。
以下のようなデータを用意します。
# 友人関係のエッジリスト
edges = [
("Alice", "Bob"),
("Alice", "Charlie"),
("Bob", "David"),
("Charlie", "David"),
("David", "Eve"),
("Eve", "Frank"),
("Frank", "Alice"),
("Charlie", "Eve")
]グラフの作成
次に、上記のエッジリストを使用してグラフを作成します。
import networkx as nx
# グラフの作成
G = nx.Graph()
G.add_edges_from(edges)中心性の計算
作成したグラフに対して、次数中心性とベットウィーンネス中心性を計算します。
# 次数中心性の計算
degree_centrality = nx.degree_centrality(G)
# ベットウィーンネス中心性の計算
betweenness_centrality = nx.betweenness_centrality(G)
# 結果の表示
print("次数中心性:")
for node, centrality in degree_centrality.items():
print(f"ノード {node}: {centrality:.2f}")
print("\nベットウィーンネス中心性:")
for node, centrality in betweenness_centrality.items():
print(f"ノード {node}: {centrality:.2f}")出力結果は以下のようになります。
次数中心性:
ノード Alice: 0.50
ノード Bob: 0.25
ノード Charlie: 0.50
ノード David: 0.50
ノード Eve: 0.50
ノード Frank: 0.25
ベットウィーンネス中心性:
ノード Alice: 0.00
ノード Bob: 0.25
ノード Charlie: 0.25
ノード David: 0.50
ノード Eve: 0.25
ノード Frank: 0.00最短経路の計算
特定のノード間の最短経路を計算します。
ここでは、AliceからFrankまでの最短経路を求めます。
# ノードAliceからノードFrankまでの最短経路を計算
shortest_path = nx.shortest_path(G, source="Alice", target="Frank")
# 結果の表示
print("\nノードAliceからノードFrankまでの最短経路:", shortest_path)出力結果は以下のようになります。
ノードAliceからノードFrankまでの最短経路: ['Alice', 'Frank']可視化
最後に、作成したグラフを可視化します。
ノードのサイズを次数に基づいて設定し、中心性を視覚的に表現します。
import matplotlib.pyplot as plt
# ノードのサイズを次数に基づいて設定
node_sizes = [G.degree(n) * 500 for n in G.nodes()]
# ネットワーク図の描画
nx.draw(G, with_labels=True, node_color='lightblue', node_size=node_sizes, font_size=16, font_color='black')
plt.title("友人関係ネットワーク")
plt.show()このように、実際のデータを使用してNetworkXを活用することで、ネットワークの分析や可視化を行うことができます。
ソーシャルネットワークの分析は、ユーザー間の関係性を理解し、さまざまな応用に役立てることができます。
NetworkXの便利な機能と拡張
NetworkXは、ネットワークの作成、可視化、分析に加えて、さまざまな便利な機能や拡張を提供しています。
ここでは、特に役立つ機能や拡張について紹介します。
グラフの種類
NetworkXでは、さまざまな種類のグラフを扱うことができます。
以下は、主なグラフの種類です。
| グラフの種類 | 説明 |
|---|---|
| 無向グラフ | エッジに方向がないグラフ |
| 有向グラフ | エッジに方向があるグラフ |
| 重み付きグラフ | エッジに重み(コスト)を持つグラフ |
| 多重グラフ | 同じノード間に複数のエッジを持つグラフ |
| サブグラフ | 元のグラフの一部を抽出したグラフ |
グラフの生成
NetworkXには、さまざまな方法でグラフを生成する機能があります。
例えば、ランダムグラフや特定の構造を持つグラフを簡単に作成できます。
以下は、ランダムグラフを生成する例です。
import networkx as nx
import matplotlib.pyplot as plt
# ランダムグラフの生成
G = nx.erdos_renyi_graph(n=10, p=0.5)
# ネットワーク図の描画
nx.draw(G, with_labels=True, node_color='lightgreen', node_size=500, font_size=10, font_color='black')
plt.title("ランダムグラフ")
plt.show()グラフの属性
ノードやエッジに属性を追加することで、より詳細な情報を持たせることができます。
以下の例では、ノードに属性を追加します。
# ノードに属性を追加
G.nodes["A"]["age"] = 25
G.nodes["B"]["age"] = 30
# 属性の表示
print("ノードAの年齢:", G.nodes["A"]["age"])
print("ノードBの年齢:", G.nodes["B"]["age"])グラフの保存と読み込み
NetworkXでは、グラフをファイルに保存したり、ファイルから読み込んだりすることができます。
以下は、グラフをGML形式で保存する例です。
# グラフの保存
nx.write_gml(G, "graph.gml")
# グラフの読み込み
G_loaded = nx.read_gml("graph.gml")拡張機能と他のライブラリとの統合
NetworkXは、他のライブラリと統合することで、さらに機能を拡張できます。
例えば、以下のようなライブラリと連携できます。
| ライブラリ名 | 説明 |
|---|---|
| Matplotlib | ネットワーク図の可視化 |
| Pandas | データフレームを使用したデータ分析 |
| SciPy | 数値計算や最適化問題の解決 |
| Graph-tool | 大規模グラフの効率的な処理 |
アルゴリズムの実装
NetworkXには、さまざまなグラフアルゴリズムが実装されています。
以下は、主なアルゴリズムの例です。
| アルゴリズム名 | 説明 |
|---|---|
| 最短経路アルゴリズム | Dijkstra法やBellman-Ford法など |
| クラスタリングアルゴリズム | K-means法や階層的クラスタリングなど |
| コミュニティ検出 | Louvain法やGirvan-Newman法など |
これらの便利な機能や拡張を活用することで、NetworkXを使ったネットワーク分析や可視化がより効果的に行えるようになります。
さまざまな機能を試して、自分のプロジェクトに最適な方法を見つけてください。
NetworkXを使う際の注意点とベストプラクティス
NetworkXは非常に強力なライブラリですが、効果的に使用するためにはいくつかの注意点とベストプラクティスがあります。
以下に、特に重要なポイントをまとめました。
メモリ管理
大規模なグラフを扱う際には、メモリの使用量に注意が必要です。
NetworkXは、ノードやエッジの数が増えるとメモリを大量に消費することがあります。
以下の対策を考慮してください。
- サンプリング: 大規模なグラフからサンプルを抽出して分析する。
- データ型の選択: 必要に応じて、軽量なデータ構造を使用する(例:
DiGraphやMultiGraphなど)。
アルゴリズムの選択
NetworkXには多くのアルゴリズムが実装されていますが、アルゴリズムによっては計算時間が長くなることがあります。
以下の点に注意してください。
- 計算量の理解: 使用するアルゴリズムの計算量を理解し、適切なアルゴリズムを選択する。
- 最適化: 必要に応じて、アルゴリズムのパラメータを調整してパフォーマンスを向上させる。
データの整合性
グラフを構築する際には、データの整合性を保つことが重要です。
以下の点に注意してください。
- 重複ノードの回避: 同じノードを複数回追加しないようにする。
- エッジの重み: 重み付きグラフを使用する場合、エッジの重みが正確であることを確認する。
可視化の工夫
可視化は、ネットワークの理解を深めるために重要ですが、適切な可視化手法を選ぶことが必要です。
以下のポイントを考慮してください。
- ノードのサイズと色: ノードのサイズや色を使って、重要な情報を強調する。
- レイアウトの選択: グラフの構造に応じて適切なレイアウトを選択する(例:
spring_layoutやcircular_layoutなど)。
ドキュメントとコミュニティの活用
NetworkXの公式ドキュメントやコミュニティを活用することで、問題解決や新しいアイデアを得ることができます。
以下のリソースを活用してください。
- 公式ドキュメント: NetworkXの公式ドキュメントを参照して、機能や使い方を確認する。
- フォーラムやGitHub: 問題が発生した場合は、フォーラムやGitHubのリポジトリで質問や情報を探す。
バージョン管理
NetworkXは定期的に更新されており、新しい機能やバグ修正が行われています。
以下の点に注意してください。
- バージョンの確認: 使用しているNetworkXのバージョンを確認し、最新の機能を活用する。
- 互換性の確認: 他のライブラリとの互換性を確認し、必要に応じてバージョンを調整する。
これらの注意点とベストプラクティスを考慮することで、NetworkXをより効果的に活用し、ネットワーク分析や可視化の精度を向上させることができます。
まとめ
この記事では、NetworkXを使用したネットワーク図の作成、可視化、分析の方法について詳しく解説しました。
また、実際のデータを用いた応用例や、便利な機能、注意点、ベストプラクティスについても触れました。
これらの情報を活用することで、ネットワーク分析のスキルを向上させ、さまざまなプロジェクトに応用することが可能です。
ぜひ、NetworkXを使って自分自身のネットワークデータを分析し、新たな発見をしてみてください。

![[Python] 自作モジュールではutils.pyのような名前は使用しないほうがいい](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46890.png)
![[Python] retryモジュールの使い方 – リトライ制御の簡略化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46889.png)
![[Python] numbaの使い方 – Pythonコードの高速化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46886.png)
![[Python] Pillow(PILの後継ライブラリ)の使い方 – シンプルな画像処理ライブラリ](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46888.png)
![[Python] Open3Dライブラリの使い方 – 3D(ポリゴンやモデルデータ)処理](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46887.png)
![[Python] scipy.optimize.minimizeの使い方 – 目的関数の最小化](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46884.png)

![[Python] matplotlibの使い方 – グラフ描画でデータを可視化する](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46883.png)
![[Python] graphvizライブラリの使い方 – 高品質なグラフの描画](https://af-e.net/wp-content/uploads/2024/10/thumbnail-46882.png)
