OpenCV

【C++】OpenCVで実現するエッジ検出のシンプル実践テクニックと応用例

2025-04-22更新日: 2025-04-22

OpenCVとC++を使ったエッジ検出は、画像の輪郭や形状を抽出する簡単で効果的な手法です。

主要な関数としては、cv::Sobel、cv::Laplacian、cv::Cannyがあり、各手法には特性があるため、目的に合わせた選択が可能です。

直感的なコード実装で、高速な画像処理が実現できるため、実用的な画像解析に適しています。

目次から探す

エッジ検出手法の基礎と特徴
パラメータ設定と調整のポイント
手法別結果の比較と応用事例
- 結果品質の評価
- 応用事例の検討
課題と改善の展望
- 現状手法の課題
- 改善策と今後の可能性
まとめ

エッジ検出手法の基礎と特徴

Sobel法の基本原理

Sobel法は、画像の輝度変化を捉えるために水平方向と垂直方向の勾配を計算するシンプルな方法です。

勾配は、画像内の急激な輝度変化箇所を強調し、エッジ情報を抽出する手法として多くの場面で採用されています。

サンプルコードでは、cv::Sobel関数を用いて画像の左右や上下のエッジを求める方法を示しています。

水平・垂直方向の演算メカニズム

Sobelフィルタでは、画像に対して水平方向と垂直方向それぞれの微分を行う演算子が適用されます。

例えば、水平および垂直の勾配を求める際には次のようなカーネルが利用されます。

水平方向カーネル例

$[\begin{matrix} - 1 & 0 & + 1 \\ - 2 & 0 & + 2 \\ - 1 & 0 & + 1 \end{matrix}]$

垂直方向カーネル例

$[\begin{matrix} - 1 & - 2 & - 1 \\ 0 & 0 & 0 \\ + 1 & + 2 & + 1 \end{matrix}]$

以下は、Sobel法によるエッジ検出のサンプルコードです。

コード中の変数名は英語表記、コメントは日本語で記述しています。

#include <opencv2/opencv.hpp>
#include <iostream>
int main() {
    // 画像ファイルをグレースケールで読み込みます
    cv::Mat image = cv::imread("sample.jpg", cv::IMREAD_GRAYSCALE);
    if (image.empty()) {
        std::cerr << "画像の読み込みに失敗しました" << std::endl;
        return -1;
    }
    // 水平方向と垂直方向の勾配を計算します
    cv::Mat gradX, gradY, gradMagnitude;
    cv::Sobel(image, gradX, CV_32F, 1, 0, 3);  // x方向の勾配
    cv::Sobel(image, gradY, CV_32F, 0, 1, 3);  // y方向の勾配
    // 勾配の大きさを計算します
    cv::magnitude(gradX, gradY, gradMagnitude);
    // 結果として得られた勾配を8ビットに変換し表示します
    cv::Mat displayImage;
    gradMagnitude.convertTo(displayImage, CV_8U);
    cv::imshow("Sobel Gradient", displayImage);
    cv::waitKey(0);
    return 0;
}

(ウィンドウにエッジが強調された画像が表示される)

このサンプルコードは、画像の水平方向と垂直方向のエッジ情報を得る基本的な流れを提供しており、画像中のオブジェクトの輪郭抽出に有効です。

カーネルサイズと処理効果

Sobel法ではカーネルサイズがエッジ検出の結果に大きく影響します。

小さいカーネルサイズ(通常3×3)を使うと細かいエッジを捉えやすくなりますが、ノイズの影響を受けやすくなる傾向があります。

一方、大きなカーネルサイズを利用すると平滑効果が強まり、ノイズの影響が和らぎますが、細部のエッジがぼやける可能性があります。

したがって、処理対象の画像の特性に応じて適切なカーネルサイズを選択することが重要です。

Laplacian法の基本原理

Laplacian法は、画像の2次微分を計算することでエッジ箇所を強調する手法です。

1次微分のSobel法とは異なり、2次微分を使用するため、エッジ付近の急激な変化がより強調される傾向があります。

画像の輪郭に沿った変化が際立つため、シンプルなエッジ検出の手段として採用されることが多いです。

2次微分による境界強調の仕組み

Laplacian法は、画像上の各画素に対して2次微分を計算します。

ガウス関数などで平滑化した後、以下のようなカーネルによって2次微分が行われます。

$[\begin{matrix} 0 & 1 & 0 \\ 1 & - 4 & 1 \\ 0 & 1 & 0 \end{matrix}]$

この演算では、中心の画素と周囲の画素との差が計算され、急激な変化が大きな値として現れます。

これにより、エッジ部分の境界が明確になります。

出力特性と注意点

Laplacian法の出力は、正負の値を含む場合があるため、そのまま表示するとゼロを中心としたコントラストが低い結果になることがあります。

多くの場合、出力値を8ビットに変換するための処理が必要となります。

また、2次微分はノイズに対する感度が高いため、画像の平滑化処理(ガウシアンブラーなど)を併用することが推奨されます。

以下は、Laplacian法によるエッジ検出のサンプルコードです。

#include <opencv2/opencv.hpp>
#include <iostream>
int main() {
    // 画像ファイルをグレースケールで読み込みます
    cv::Mat image = cv::imread("sample.jpg", cv::IMREAD_GRAYSCALE);
    if (image.empty()) {
        std::cerr << "画像の読み込みに失敗しました" << std::endl;
        return -1;
    }
    // Laplacianフィルタで2次微分を計算します
    cv::Mat laplacianImage;
    cv::Laplacian(image, laplacianImage, CV_32F, 3);
    // 結果を8ビットに変換して表示します
    cv::Mat displayImage;
    laplacianImage.convertTo(displayImage, CV_8U);
    cv::imshow("Laplacian Gradient", displayImage);
    cv::waitKey(0);
    return 0;
}

平滑化処理と併用することで、ノイズの影響を低減しつつエッジを強調できる点がLaplacian法の魅力です。

Canny法の基本原理

Canny法は、多段階の処理を経て高精度なエッジの抽出を実現する手法です。

まずノイズを低減するための平滑化処理が行われ、次に輝度の勾配計算、非最大抑制、そしてエッジの紐付け(ヒステリシス処理)が適用されます。

これにより、他の手法と比べて滑らかなエッジが得られる傾向があります。

エッジ抽出プロセスの流れ

Canny法の処理は、大きく次のステップに分かれます。

画像の前処理としてガウシアンフィルタでノイズを除去する
画像の輝度勾配を計算する
非最大抑制により、勾配方向に沿った局所最大値のみを残す
低閾値と高閾値によるヒステリシス処理を行い、強いエッジと弱いエッジを判定する

このプロセスにより、エッジ検出の精度が向上し、細部の情報が失われにくくなります。

ヒステリシス処理と閾値設定の役割

Canny法の特徴的な処理であるヒステリシス処理は、低閾値と高閾値を用いたエッジの判定に重きを置きます。

具体的には、高閾値を超える画素は確実なエッジとみなし、低閾値を超えるが高閾値に達さなかった画素は、近傍に強いエッジが存在する場合にのみエッジと認識されます。

この仕組みにより、細かいエッジも取りこぼさずに抽出できる可能性が広がります。

以下は、Canny法によるエッジ検出のサンプルコードです。

#include <opencv2/opencv.hpp>
#include <iostream>
int main() {
    // 画像ファイルをグレースケールで読み込みます
    cv::Mat image = cv::imread("sample.jpg", cv::IMREAD_GRAYSCALE);
    if (image.empty()) {
        std::cerr << "画像の読み込みに失敗しました" << std::endl;
        return -1;
    }
    // ノイズ除去としてガウシアンブラーを適用します
    cv::Mat blurred;
    cv::GaussianBlur(image, blurred, cv::Size(5, 5), 1.5);
    // Canny法によるエッジ検出を実施します
    cv::Mat edges;
    cv::Canny(blurred, edges, 50, 150);
    // 検出結果を表示します
    cv::imshow("Canny Edges", edges);
    cv::waitKey(0);
    return 0;
}

(ウィンドウに細かいエッジまで抽出された画像が表示される)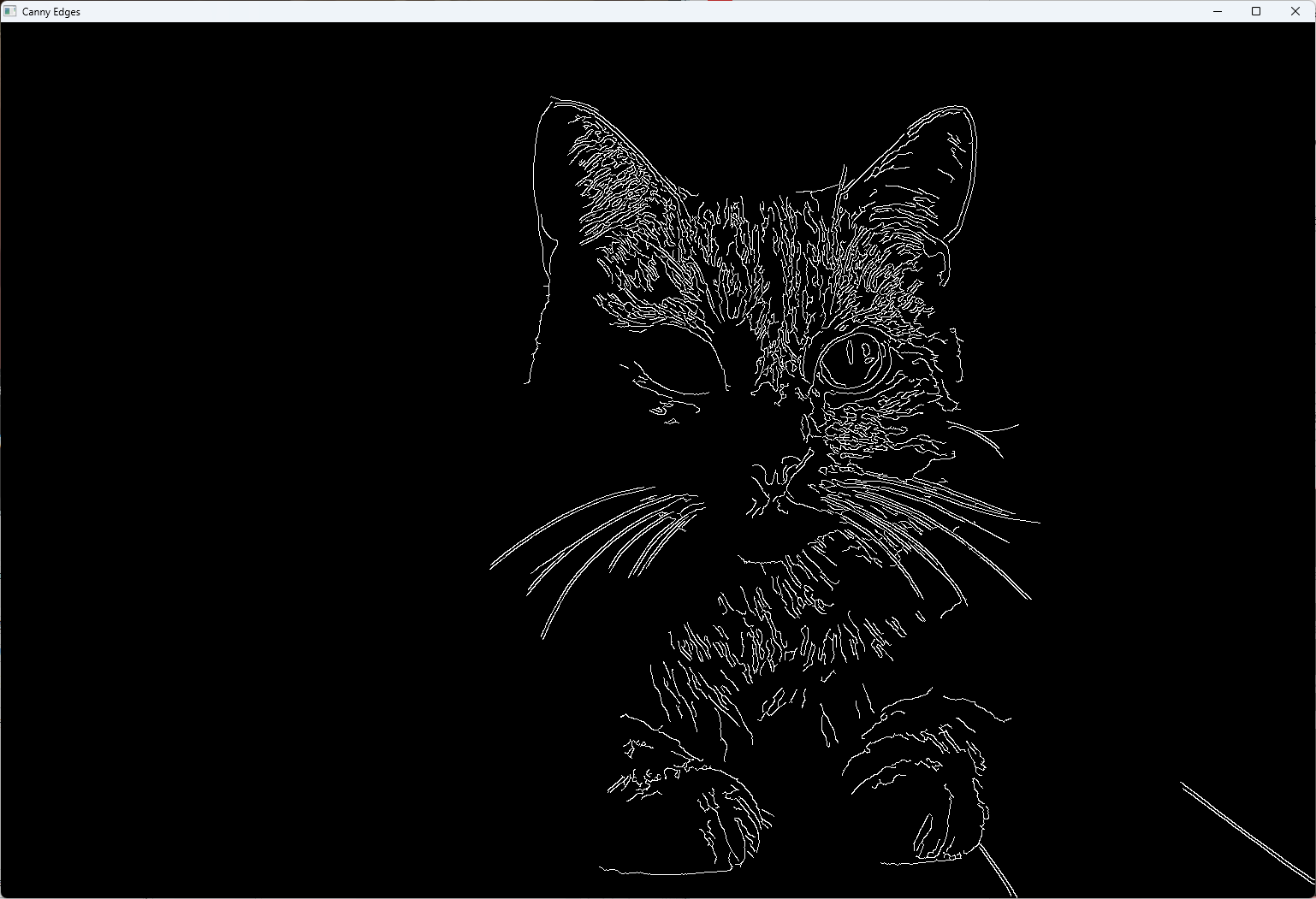

Canny法は各工程の工夫により、高精度なエッジ検出が可能となっており、複雑な画像解析タスクに役立つ手法です。

パラメータ設定と調整のポイント

Sobel法のパラメータ調整

Sobel法はシンプルながらも、カーネルサイズや演算方向の指定など、パラメータの調整が結果に大きく影響する手法です。

演算方向とカーネルサイズの選定

演算方向はdxとdyの設定で指定し、抽出するエッジの向きを決定します.

水平方向のエッジ検出の場合、dx=1、dy=0の設定が一般的です.
垂直方向のエッジ検出の場合、dx=0、dy=1となります.

また、カーネルサイズは通常3×3が標準的ですが、画像に含まれるノイズ量やエッジの細かさに応じて、サイズの変更を検討することが望ましいです。

出力型と境界処理の検討

計算結果の出力型としては、通常CV_32Fが用いられますが、表示する際に8ビットに変換する必要があります. また、境界部ではエッジ検出の計算が不完全になる可能性があるため、cv::BORDER_DEFAULTなどの境界補完オプションを利用する方法も検討できます。

Laplacian法のパラメータ調整

Laplacian法のパラメータ調整は、特にオペレータサイズと事前の平滑化処理の連動に留意する必要があります。

オペレータサイズの最適化

オペレータサイズは、カーネルの窓の大きさを表し、通常3×3が推奨されます. 画像の特性に応じて、より大きなサイズに変更することで、エッジ検出後の結果が滑らかになる反面、細かいエッジが失われる可能性もあるため、慎重な調整が求められます.

平滑化処理との連動性

Laplacianではノイズに敏感なため、事前にガウシアンブラーなどで画像を平滑化する手法が有効です. 平滑処理のカーネルサイズや標準偏差などのパラメータとLaplacianのオペレータサイズとのバランスをとることで、検出結果が向上します.

Canny法のパラメータ調整

Canny法のエッジ検出では、低閾値と高閾値の設定が検出結果に直接影響するため、適切な値の選定が重要です。

低閾値・高閾値の設定基準

低閾値と高閾値は、エッジを抽出するためのしきい値として機能します. 通常、高閾値は強いエッジを示す画素を選び、低閾値は近傍の弱いエッジを補完的に抽出します.

低閾値が高すぎると、一部の弱いエッジが検出されなくなる可能性があります.
逆に低閾値が低すぎると、ノイズまでエッジとして抽出されやすくなります.

これらの閾値設定は、画像ごとの特性に合わせて実験的に調整することがおすすめです.

エッジ連結性確保の工夫

ヒステリシス処理を用いることで、連続したエッジが正しく識別されるよう工夫されています.

ヒステリシスでは、高閾値を超える画素を中心とし、再度周囲の画素も判定する仕組みを採用します.
これにより、不連続なエッジが補完され、全体として滑らかな輪郭が得られるようになります.

適切な閾値の設定と平滑処理の併用が、エッジ連結性の向上に大きく寄与します.

手法別結果の比較と応用事例

各エッジ検出手法には特徴があり、その結果や応用事例も多岐にわたります。

手法ごとの比較を通じて、最適な方法を選ぶ際の参考になる情報が得られます.

結果品質の評価

検出結果の品質評価は、主にノイズの影響や計算速度とのバランスの観点から考えられます.

ノイズ影響と対策

Sobel法

ノイズに対して比較的敏感なため、前処理としてガウシアンフィルタなどの平滑化が有効です.

Laplacian法

2次微分の性質上、微小なノイズが大きく表れるため、必ず事前の平滑化処理を組み合わせる必要があります.

Canny法

初期の平滑化処理が組み込まれているため、ノイズに対する耐性が強化されています.

精度と速度のバランス検討

Sobel法はシンプルな計算のため処理速度が速く、リアルタイムアプリケーションにも適しています.
Laplacian法は、エッジの強調が明確ですが、平滑化との組み合わせで多少処理負荷が増える可能性があります.
Canny法は、多段階の処理を行うため計算量は増えますが、エッジの精度と連続性の点で高評価を得やすいです.

応用事例の検討

エッジ検出は画像解析ワークフローの一部として、また自動認識システムへの入力前処理として幅広く利用されます.

画像解析ワークフローでの役割

エッジ検出は、以下のような役割を果たします。

物体輪郭の抽出
特徴点検出や形状認識の前段階としての利用
画像セグメンテーションの補助

これらの処理を通して、最終的な画像解析の精度アップに貢献します.

自動認識システムへの適用

自動運転や監視システムなどの分野でも、エッジ検出は重要な役割を果たします.

車両や歩行者の輪郭抽出に用いられ、対象の認識精度を向上させる役割を担います.
エッジ情報は、パターン認識や機械学習アルゴリズムの入力として利用されることが多く、精度向上に寄与します.

課題と改善の展望

エッジ検出手法には多くの実用例がある一方で、いくつかの課題も存在します。

さらなる改善のための研究や実装上の工夫が求められています.

現状手法の課題

各手法が抱える課題に対する理解は、改善策を講じる上でも役立ちます.

誤検出・不足検出の主な原因

Sobel法とLaplacian法

ノイズの影響によって誤ったエッジが検出されたり、微細なエッジが抽出されなかったりすることがあります.

Canny法

閾値設定が適切でない場合、弱いエッジが取りこぼされる危険がある他、誤検出も生じる可能性があります.

環境依存性の影響

照明条件や画像のコントラスト、解像度などの環境依存性が、エッジ検出結果に大きな影響を与えることも確認されており、これらの要因を十分に考慮する必要があります.

改善策と今後の可能性

エッジ検出の精度と安定性の向上のために、さまざまな改善策が検討されています.

事前処理技術の応用事例

画像の平滑化処理は、エッジ検出の前段階として有効な手段です.

ガウシアンブラー以外にも、メディアンフィルタや双方向フィルタなど、ノイズ除去とエッジを保持するバランスがとれる手法が研究されています.
これらの手法を組み合わせることで、誤検出の軽減や細かいエッジ抽出の改善が期待できます.

他手法との組み合わせによる向上効果

エッジ検出単体だけでなく、他の画像特徴抽出手法との組み合わせが検討されています.

例えば、Sobel法やLaplacian法で得られたエッジ情報を、Canny法の結果と融合することにより、より精度の高いエッジ抽出が可能になる場合があります.
また、機械学習のアルゴリズムと組み合わせることで、環境の変化に柔軟に対応できるエッジ検出システムの構築も実現可能です.

まとめ

今回の記事では、各エッジ検出手法の基本的な原理とパラメータの調整方法、そして結果の評価と応用事例について解説を進めました。

Sobel法、Laplacian法、Canny法がそれぞれ異なる特徴を持ち、処理速度や精度、ノイズへの影響などの面で特徴が分かれる点が興味深いです。

さらに、手法同士を組み合わせることで、実問題に応じた最適なエッジ検出が可能なシステムの構築に向けた取り組みが期待できる内容となりました。

今後も適切なパラメータの調整や新たな前処理技術の導入、そして組み合わせ手法の実用化を通して、より洗練されたエッジ検出が進むと考えられます。