[C言語] c曲線の生成と描画方法

2025-04-15更新日: 2025-04-15

C言語でc曲線を生成し描画するには、再帰的な手法を用いるのが一般的です。

c曲線はフラクタルの一種で、直線を特定のルールに従って繰り返し分割し、曲線を形成します。

まず、初期の直線を定義し、再帰関数を使ってその直線を2つの短い直線に分割し、特定の角度で配置します。

このプロセスを指定した回数だけ繰り返すことで、c曲線が形成されます。

描画には、グラフィックスライブラリ(例: SDLやOpenGL)を使用して、計算された座標に基づいて線を描画します。

再帰の深さを調整することで、曲線の複雑さを制御できます。

目次から探す

c曲線とは
C言語でのc曲線生成
c曲線の描画方法
応用例
まとめ

c曲線とは

c曲線は、フラクタルの一種であり、自己相似性を持つ幾何学的な図形です。

フラクタルは、部分が全体と同じ形状を持つという特性を持ち、自然界や数学の中で多くの応用があります。

c曲線は、その美しい形状と数学的な特性から、コンピュータグラフィックスやアートの分野で注目されています。

フラクタルの基本

フラクタルは、自己相似性を持つ図形であり、どの部分を拡大しても全体と同じ形状を持つという特徴があります。

フラクタルの基本的な概念は、以下の通りです。

特徴	説明
自己相似性	部分が全体と同じ形状を持つ
無限の複雑さ	拡大しても常に新しい詳細が現れる
非整数次元	フラクタル次元と呼ばれる、通常の次元とは異なる次元を持つ

フラクタルは、自然界の多くの現象をモデル化するために使用され、例えば、海岸線の形状や雲の形状などが挙げられます。

c曲線の歴史と背景

c曲線は、数学者のヘルマン・ワイルによって考案されました。

彼は、フラクタルの概念を用いて、無限に複雑な曲線を生成する方法を研究しました。

c曲線は、単純な直線を繰り返し分割し、特定の角度で回転させることで生成されます。

この手法は、フラクタルの生成における基本的なアプローチの一つです。

c曲線は、コンピュータの発展とともに、グラフィックスの分野で広く利用されるようになりました。

特に、コンピュータアートやデジタルデザインにおいて、その美しい形状が多くのアーティストにインスピレーションを与えています。

c曲線の数学的特性

c曲線の数学的特性は、以下のようにまとめられます。

特性	説明
自己相似性	繰り返し分割と回転により、全体と同じ形状を持つ部分が生成される
フラクタル次元	通常の次元とは異なる、非整数次元を持つ
無限の長さ	再帰的に生成されるため、理論上は無限の長さを持つ

c曲線は、数学的に興味深いだけでなく、視覚的にも魅力的な図形です。

その生成過程は、プログラミングによって容易に再現できるため、教育や研究の場でも活用されています。

C言語でのc曲線生成

C言語を用いてc曲線を生成するには、再帰的なアルゴリズムを実装する必要があります。

ここでは、必要なライブラリや環境設定、再帰関数の基本、そしてc曲線の生成アルゴリズムについて詳しく解説します。

必要なライブラリと環境設定

c曲線を描画するためには、グラフィックスライブラリが必要です。

C言語で一般的に使用されるライブラリには、SDLやOpenGLがあります。

ここでは、SDLを使用した環境設定について説明します。

SDLのインストール: SDLは、クロスプラットフォームのグラフィックスライブラリで、簡単に2Dグラフィックスを描画できます。

インストールは、各OSのパッケージマネージャーを使用するか、公式サイトからダウンロードして行います。

コンパイラの設定: SDLを使用するためには、コンパイラにライブラリのパスを指定する必要があります。

例えば、GCCを使用する場合、-lSDL2オプションを追加します。

再帰関数の基本

再帰関数は、関数が自分自身を呼び出すことで、問題を小さく分割して解決する手法です。

c曲線の生成には、再帰関数が不可欠です。

以下に、再帰関数の基本的な構造を示します。

#include <stdio.h>
// 再帰関数の例
void recursiveFunction(int n) {
    if (n <= 0) {
        return; // 基底条件
    }
    printf("n = %d\n", n);
    recursiveFunction(n - 1); // 再帰呼び出し
}
int main() {
    recursiveFunction(5);
    return 0;
}

この例では、recursiveFunctionが自分自身を呼び出し、nが0以下になるまで繰り返します。

c曲線のアルゴリズム

c曲線を生成するためのアルゴリズムは、初期直線を分割し、特定の角度で回転させることで構成されます。

以下に、各ステップを詳しく説明します。

初期直線の定義

c曲線の生成は、まず初期直線を定義することから始まります。

この直線は、c曲線の最初の形状を決定します。

通常、直線は2つの点(始点と終点)で表されます。

typedef struct {
    double x;
    double y;
} Point;
void drawInitialLine(Point start, Point end) {
    // 初期直線を描画する処理
}

分割と回転の手法

初期直線を分割し、各セグメントを特定の角度で回転させることで、c曲線の形状を作り出します。

分割数や回転角度は、c曲線の形状に大きく影響します。

void divideAndRotate(Point start, Point end, int depth) {
    if (depth <= 0) {
        // 直線を描画
        return;
    }
    // 直線を分割し、回転させる処理
}

再帰の深さとその影響

再帰の深さは、c曲線の複雑さを決定します。

深さが増すほど、c曲線はより複雑で詳細な形状になりますが、計算量も増加します。

適切な深さを選ぶことが重要です。

int main() {
    Point start = {0.0, 0.0};
    Point end = {1.0, 0.0};
    int depth = 5; // 再帰の深さ
    divideAndRotate(start, end, depth);
    return 0;
}

再帰の深さを調整することで、c曲線の詳細度をコントロールできます。

深さが大きいほど、より細かいc曲線が生成されますが、描画に時間がかかることがあります。

c曲線の描画方法

c曲線を描画するためには、適切なグラフィックスライブラリを選択し、座標計算や色の設定を行う必要があります。

ここでは、SDLを使用したc曲線の描画方法について詳しく解説します。

グラフィックスライブラリの選択

c曲線を描画するためのグラフィックスライブラリには、SDLやOpenGLなどがあります。

それぞれの特徴を理解し、目的に応じて選択することが重要です。

SDLの利用

SDL(Simple DirectMedia Layer)は、2Dグラフィックスを簡単に扱えるクロスプラットフォームのライブラリです。

以下に、SDLを使用したc曲線の描画手順を示します。

SDLの初期化: SDLを使用するためには、まず初期化を行います。
ウィンドウとレンダラーの作成: 描画を行うためのウィンドウとレンダラーを作成します。
描画処理: c曲線を描画するための座標計算と描画を行います。
クリーンアップ: 使用したリソースを解放し、SDLを終了します。

#include <SDL2/SDL.h>
#include <stdio.h>
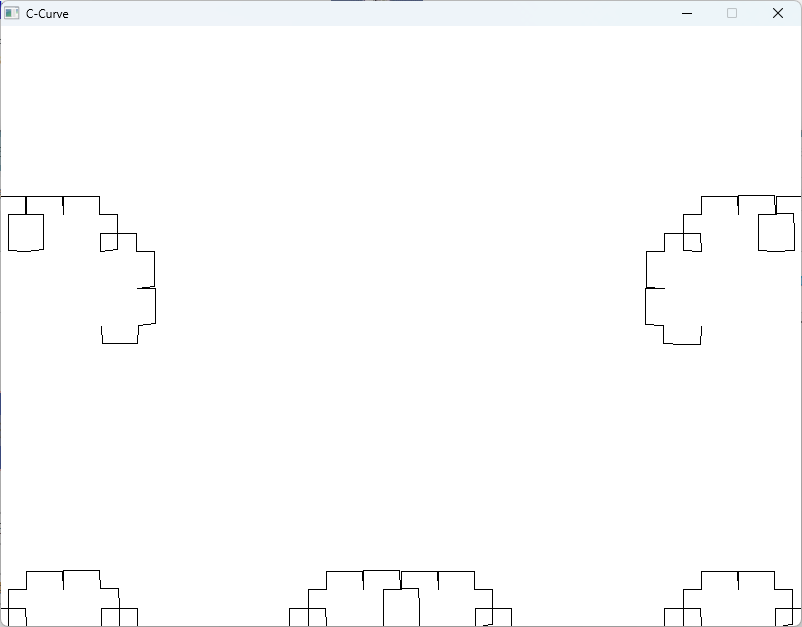
void drawCcurve(SDL_Renderer *renderer, int x1, int y1, int x2, int y2, int depth) {
    if (depth == 0) {
        SDL_RenderDrawLine(renderer, x1, y1, x2, y2);
    } else {
        int xm = (x1 + x2) / 2;
        int ym = (y1 + y2) / 2;
        int dx = (y2 - y1) / 2;
        int dy = (x2 - x1) / 2;
        drawCcurve(renderer, x1, y1, xm - dx, ym + dy, depth - 1);
        drawCcurve(renderer, xm - dx, ym + dy, x2, y2, depth - 1);
    }
}
int main() {
    SDL_Init(SDL_INIT_VIDEO);
    SDL_Window *window = SDL_CreateWindow("C-Curve", SDL_WINDOWPOS_UNDEFINED, SDL_WINDOWPOS_UNDEFINED, 800, 600, 0);
    SDL_Renderer *renderer = SDL_CreateRenderer(window, -1, SDL_RENDERER_ACCELERATED);
    SDL_SetRenderDrawColor(renderer, 255, 255, 255, 255);
    SDL_RenderClear(renderer);
    SDL_SetRenderDrawColor(renderer, 0, 0, 0, 255);
    drawCcurve(renderer, 100, 300, 700, 300, 10);
    SDL_RenderPresent(renderer);
    SDL_Delay(5000);
    SDL_DestroyRenderer(renderer);
    SDL_DestroyWindow(window);
    SDL_Quit();
    return 0;
}