[C言語] Lorenzアトラクタのシミュレーションと可視化方法
Lorenzアトラクタは、気象学者エドワード・ローレンツが提案したカオス理論の一例で、3次元の非線形微分方程式系によって記述されます。
C言語でシミュレーションするには、オイラー法やルンゲ・クッタ法などの数値積分法を用いて微分方程式を解きます。
具体的には、時間ステップを設定し、各ステップでx, y, zの値を更新します。
可視化には、生成したデータをPythonのMatplotlibやGnuplotなどの外部ツールに渡してプロットします。
これにより、特有の蝶形の軌道を描くことができます。
Lorenzアトラクタとは
Lorenzアトラクタの歴史と背景
Lorenzアトラクタは、1963年にアメリカの気象学者エドワード・ローレンツによって発見されました。
彼は気象予測のための簡略化された数値モデルを研究している際に、このアトラクタを見つけました。
ローレンツの研究は、気象の予測がいかに困難であるかを示し、カオス理論の発展に大きく寄与しました。
彼の発見は、初期条件のわずかな違いが結果に大きな影響を与えることを示し、「バタフライ効果」としても知られています。
カオス理論におけるLorenzアトラクタの位置づけ
カオス理論は、非線形動的システムの挙動を研究する数学の一分野です。
Lorenzアトラクタは、この理論の中で最も有名な例の一つです。
カオス理論では、システムが予測不可能でありながらも、ある種の秩序を持つことが示されています。
Lorenzアトラクタは、決定論的なシステムでありながら、長期的な予測が不可能であることを示す典型的な例です。
このアトラクタは、三次元空間における軌道が複雑な形状を描くことで知られています。
Lorenzアトラクタの数学的定義
Lorenzアトラクタは、以下の三つの微分方程式で定義されます。
- \(\frac{dx}{dt} = \sigma (y – x)\)
- \(\frac{dy}{dt} = x (\rho – z) – y\)
- \(\frac{dz}{dt} = xy – \beta z\)
ここで、\(\sigma\)、\(\rho\)、\(\beta\)はシステムのパラメータであり、通常は\(\sigma = 10\)、\(\rho = 28\)、\(\beta = \frac{8}{3}\)が用いられます。
これらの方程式は、流体の対流をモデル化したもので、特に気象学における対流現象を表現しています。
Lorenzアトラクタは、これらの方程式の解として得られる軌道が、初期条件に非常に敏感であることを示しています。
C言語によるLorenzアトラクタのシミュレーション
必要なライブラリと環境設定
C言語でLorenzアトラクタをシミュレーションするためには、特別なライブラリは必要ありませんが、数値計算を行うために標準ライブラリのmath.hを使用します。
また、結果を可視化するために、データをファイルに出力し、後で可視化ツール(例:PythonのMatplotlibやGnuplot)を使用することが一般的です。
開発環境としては、GCCやClangなどのCコンパイラが必要です。
Lorenz方程式の実装
Lorenz方程式をC言語で実装するには、微分方程式を数値的に解く必要があります。
以下に、基本的な構造を示します。
#include <stdio.h>
#include <math.h>
// Lorenz方程式のパラメータ
#define SIGMA 10.0
#define RHO 28.0
#define BETA (8.0 / 3.0)
// Lorenz方程式の計算
void lorenz(double x, double y, double z, double *dx, double *dy, double *dz) {
*dx = SIGMA * (y - x);
*dy = x * (RHO - z) - y;
*dz = x * y - BETA * z;
}数値積分法の選択と実装
数値積分法は、微分方程式を解くための手法です。
Lorenzアトラクタのシミュレーションでは、オイラー法やルンゲ・クッタ法がよく使用されます。
オイラー法の概要と実装
オイラー法は、最も基本的な数値積分法の一つで、計算が簡単ですが精度が低いという特徴があります。
以下にオイラー法を用いた実装例を示します。
void euler(double *x, double *y, double *z, double dt) {
double dx, dy, dz;
lorenz(*x, *y, *z, &dx, &dy, &dz);
*x += dx * dt;
*y += dy * dt;
*z += dz * dt;
}ルンゲ・クッタ法の概要と実装
ルンゲ・クッタ法は、オイラー法よりも精度が高い数値積分法です。
特に4次のルンゲ・クッタ法(RK4)は、精度と計算コストのバランスが良いため、広く使用されています。
void runge_kutta(double *x, double *y, double *z, double dt) {
double dx1, dy1, dz1, dx2, dy2, dz2, dx3, dy3, dz3, dx4, dy4, dz4;
double x_temp, y_temp, z_temp;
lorenz(*x, *y, *z, &dx1, &dy1, &dz1);
x_temp = *x + 0.5 * dx1 * dt;
y_temp = *y + 0.5 * dy1 * dt;
z_temp = *z + 0.5 * dz1 * dt;
lorenz(x_temp, y_temp, z_temp, &dx2, &dy2, &dz2);
x_temp = *x + 0.5 * dx2 * dt;
y_temp = *y + 0.5 * dy2 * dt;
z_temp = *z + 0.5 * dz2 * dt;
lorenz(x_temp, y_temp, z_temp, &dx3, &dy3, &dz3);
x_temp = *x + dx3 * dt;
y_temp = *y + dy3 * dt;
z_temp = *z + dz3 * dt;
lorenz(x_temp, y_temp, z_temp, &dx4, &dy4, &dz4);
*x += (dx1 + 2*dx2 + 2*dx3 + dx4) * dt / 6.0;
*y += (dy1 + 2*dy2 + 2*dy3 + dy4) * dt / 6.0;
*z += (dz1 + 2*dz2 + 2*dz3 + dz4) * dt / 6.0;
}これらの数値積分法を用いることで、Lorenzアトラクタの軌道をシミュレーションすることができます。
オイラー法は計算が簡単ですが、精度が低いため、より精度が必要な場合はルンゲ・クッタ法を使用することが推奨されます。
シミュレーション結果の可視化
データの出力方法
C言語でシミュレーションしたLorenzアトラクタの結果を可視化するためには、まずデータをファイルに出力する必要があります。
以下に、シミュレーション結果をCSV形式でファイルに保存する方法を示します。
#include <math.h>
#include <stdio.h>
// Lorenz方程式のパラメータ
#define SIGMA 10.0
#define RHO 28.0
#define BETA (8.0 / 3.0)
// Lorenz方程式の計算
void lorenz(double x, double y, double z, double *dx, double *dy, double *dz) {
*dx = SIGMA * (y - x);
*dy = x * (RHO - z) - y;
*dz = x * y - BETA * z;
}
void runge_kutta(double *x, double *y, double *z, double dt) {
double dx1, dy1, dz1, dx2, dy2, dz2, dx3, dy3, dz3, dx4, dy4, dz4;
double x_temp, y_temp, z_temp;
lorenz(*x, *y, *z, &dx1, &dy1, &dz1);
x_temp = *x + 0.5 * dx1 * dt;
y_temp = *y + 0.5 * dy1 * dt;
z_temp = *z + 0.5 * dz1 * dt;
lorenz(x_temp, y_temp, z_temp, &dx2, &dy2, &dz2);
x_temp = *x + 0.5 * dx2 * dt;
y_temp = *y + 0.5 * dy2 * dt;
z_temp = *z + 0.5 * dz2 * dt;
lorenz(x_temp, y_temp, z_temp, &dx3, &dy3, &dz3);
x_temp = *x + dx3 * dt;
y_temp = *y + dy3 * dt;
z_temp = *z + dz3 * dt;
lorenz(x_temp, y_temp, z_temp, &dx4, &dy4, &dz4);
*x += (dx1 + 2 * dx2 + 2 * dx3 + dx4) * dt / 6.0;
*y += (dy1 + 2 * dy2 + 2 * dy3 + dy4) * dt / 6.0;
*z += (dz1 + 2 * dz2 + 2 * dz3 + dz4) * dt / 6.0;
}
// シミュレーション結果をファイルに出力
void output_data(FILE *file, double x, double y, double z) {
fprintf(file, "%f,%f,%f\n", x, y, z);
}
int main() {
FILE *file = fopen("lorenz_data.csv", "w");
if (file == NULL) {
perror("ファイルを開けません");
return 1;
}
double x = 1.0, y = 1.0, z = 1.0;
double dt = 0.01;
int steps = 10000;
for (int i = 0; i < steps; i++) {
runge_kutta(&x, &y, &z, dt);
output_data(file, x, y, z);
}
fclose(file);
return 0;
}このコードは、シミュレーションの各ステップで計算された\(x\)、\(y\)、\(z\)の値をlorenz_data.csvというファイルに出力します。
Pythonを用いた可視化
Pythonは、データの可視化に非常に便利なライブラリを提供しています。
特に、Matplotlibを使用すると、簡単に3Dプロットを作成できます。
以下に、Pythonを用いてLorenzアトラクタを可視化する方法を示します。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import pandas as pd
# CSVファイルからデータを読み込む
data = pd.read_csv('lorenz_data.csv', header=None, names=['x', 'y', 'z'])
# 3Dプロットの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(data['x'], data['y'], data['z'])
ax.set_xlabel('X 軸')
ax.set_ylabel('Y 軸')
ax.set_zlabel('Z 軸')
plt.title('Lorenzアトラクタの3Dプロット')
plt.show()このスクリプトは、CSVファイルからデータを読み込み、3Dプロットを作成します。
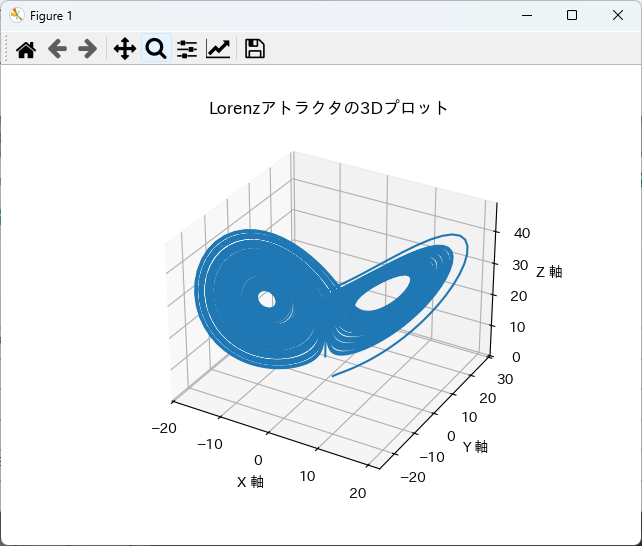
MatplotlibのAxes3Dを使用して、Lorenzアトラクタの軌道を視覚的に確認できます。
Gnuplotを用いた可視化
Gnuplotは、コマンドラインベースのプロットツールで、簡単にデータを可視化できます。
以下に、Gnuplotを用いてLorenzアトラクタを可視化する方法を示します。
まず、以下のコマンドをGnuplotのプロンプトで実行します。
set terminal pngcairo
set output 'lorenz_plot.png'
set xlabel 'X 軸'
set ylabel 'Y 軸'
set zlabel 'Z 軸'
splot 'lorenz_data.csv' using 1:2:3 with lines title 'Lorenzアトラクタ'このコマンドは、CSVファイルからデータを読み込み、3Dプロットを作成し、lorenz_plot.pngという画像ファイルに出力します。
Gnuplotは、シンプルなコマンドで強力な可視化を行うことができるため、データの解析に非常に便利です。
Lorenzアトラクタの応用例
気象予測への応用
Lorenzアトラクタは、もともと気象予測の研究から生まれたものであり、気象学におけるカオス理論の重要性を示しています。
気象システムは非常に複雑で、初期条件に対する感度が高いため、長期的な予測が困難です。
Lorenzアトラクタは、このようなシステムの挙動を理解するためのモデルとして利用され、気象予測の精度向上に貢献しています。
特に、短期的な予測の精度を高めるための手法として、アンサンブル予報などの技術が開発されています。
金融市場のモデリング
金融市場もまた、カオス的な挙動を示すシステムの一つです。
市場の価格変動は、複雑な要因によって影響を受け、予測が難しいことで知られています。
Lorenzアトラクタは、金融市場の動きをモデル化するための一つのアプローチとして研究されています。
特に、価格の変動パターンを分析し、リスク管理や投資戦略の策定に役立てることができます。
カオス理論を応用することで、市場の不確実性をより深く理解し、より効果的な意思決定を行うことが可能になります。
生態系シミュレーション
生態系は、多くの種が相互作用する複雑なシステムであり、カオス的な挙動を示すことがあります。
Lorenzアトラクタは、生態系の動態をシミュレーションするためのモデルとしても利用されています。
例えば、捕食者と被食者の関係や、種間競争のダイナミクスを理解するために、カオス理論を応用することができます。
これにより、生態系の安定性や多様性の維持に関する洞察を得ることができ、環境保護や資源管理の戦略に役立てることができます。
これらの応用例は、Lorenzアトラクタが単なる数学的な興味にとどまらず、実世界の複雑なシステムを理解するための強力なツールであることを示しています。
カオス理論の概念を活用することで、さまざまな分野での問題解決に貢献することが可能です。
まとめ
この記事では、Lorenzアトラクタの歴史的背景や数学的定義から始まり、C言語によるシミュレーションの実装方法、そしてその結果の可視化方法について詳しく解説しました。
Lorenzアトラクタは、気象予測や金融市場のモデリング、生態系シミュレーションなど、さまざまな分野での応用が可能であり、カオス理論の重要性を再認識させるものです。
この記事を通じて得た知識を基に、実際にLorenzアトラクタのシミュレーションを試み、さらなる探求を進めてみてはいかがでしょうか。

![[C言語] ドラゴン曲線を計算するプログラムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44015.png)
![[C言語] トポロジカルソートを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44014.png)
![[C言語] ハノイの塔を解くプログラムの作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44019.png)
![[C言語] はさみうち法(非線形方程式)を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44017.png)
![[C言語] ナップザック問題を動的計画法で解く方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44016.png)
![[C言語] フラクタル圧縮を用いた画像圧縮方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44023.png)
![[C言語] プサイ関数/ポリガンマ関数を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44022.png)
![[C言語] フィボナッチ探索を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44021.png)
![[C言語] フィボナッチ数列を求めるアルゴリズムの書き方](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44020.png)
![[C言語] ベルマンフォード法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44029.png)
![[C言語] ベータ分布を計算して乱数を生成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44028.png)
![[C言語] ベータ関数を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44027.png)