[C言語] Lissajous曲線の描画方法とその応用
Lissajous曲線は、2つの直交する単振動の合成によって描かれる曲線です。
C言語で描画するには、数学ライブラリを使用してsin関数やcos関数を利用し、xとyの座標を計算します。
具体的には、x = A * sin(a * t + δ)とy = B * sin(b * t)の式を用いて、異なるtの値に対して座標を計算し、グラフィックスライブラリを使って描画します。
応用としては、オシロスコープでの信号表示や、視覚的なパターン生成、音楽や振動の解析に利用されます。
Lissajous曲線は、周波数比や位相差によって多様な形状を生み出すため、視覚的に興味深いパターンを提供します。
Lissajous曲線とは
Lissajous曲線は、数学や物理学の分野でよく知られる曲線で、特にオシロスコープでの信号表示や視覚的なパターン生成に利用されます。
この曲線は、2つの直交する単振動の合成によって形成され、特定の条件下で美しい図形を描き出します。
Lissajous曲線の歴史
Lissajous曲線は、フランスの物理学者ジュール・アントワーヌ・リサージュ(Jules Antoine Lissajous)によって19世紀に研究されました。
彼は、音叉を用いた実験でこの曲線を初めて視覚化しました。
リサージュの研究は、音波や振動の解析において重要な役割を果たし、今日でも多くの分野で応用されています。
基本的な数学的定義
Lissajous曲線は、以下のようなパラメトリック方程式で表されます。
- \( x(t) = A \sin(at + \delta) \)
- \( y(t) = B \sin(bt) \)
ここで、\( A \)と\( B \)は振幅、\( a \)と\( b \)は周波数、\( \delta \)は位相差を表します。
これらのパラメータの組み合わせにより、曲線の形状が決定されます。
特徴と性質
Lissajous曲線の特徴と性質は以下の通りです。
| 特徴 | 説明 |
|---|---|
| 周波数比 | \( a:b \)の比率が整数比であると、曲線は閉じた形状を形成します。 |
| 位相差 | 位相差\( \delta \)が0またはπの倍数であると、曲線は対称性を持ちます。 |
| 振幅 | 振幅\( A \)と\( B \)が異なると、楕円形やその他の非対称な形状が生成されます。 |
Lissajous曲線は、これらのパラメータを調整することで、さまざまな形状を描くことができ、視覚的に非常に興味深いパターンを生成します。
これにより、科学的なデモンストレーションやアート作品の制作においても広く利用されています。
C言語でのLissajous曲線描画
C言語を用いてLissajous曲線を描画するには、数学的な計算とグラフィックスライブラリを組み合わせる必要があります。
以下では、必要なライブラリやプログラムの構造について詳しく説明します。
必要なライブラリと環境設定
Lissajous曲線を描画するためには、グラフィックスライブラリが必要です。
C言語でよく使用されるライブラリには、以下のようなものがあります。
| ライブラリ名 | 説明 |
|---|---|
| SDL | シンプルなAPIで2Dグラフィックスを描画できるライブラリ。 |
| OpenGL | 高度な3Dグラフィックスを描画するためのライブラリ。 |
| Cairo | ベクターグラフィックスを描画するためのライブラリ。 |
これらのライブラリを使用するには、開発環境にインストールし、適切に設定する必要があります。
基本的なプログラム構造
C言語でのプログラムは、以下のような基本構造を持ちます。
- 必要なヘッダファイルのインクルード
- メイン関数の定義
- 初期化処理
- 描画ループ
- 終了処理
sin関数とcos関数の利用
Lissajous曲線の描画には、math.hライブラリのsin関数とcos関数を使用します。
これらの関数を用いて、曲線の各点の座標を計算します。
#include <math.h>
// 例:sin関数とcos関数を用いた座標計算
double x = A * sin(a * t + delta);
double y = B * sin(b * t);座標計算の方法
Lissajous曲線の座標は、時間変数tを用いて計算します。
tを一定の間隔で増加させることで、曲線を描画します。
for (double t = 0; t < 2 * M_PI; t += 0.01) {
double x = A * sin(a * t + delta);
double y = B * sin(b * t);
// 描画処理
}グラフィックスライブラリの選択
描画には、前述のグラフィックスライブラリを選択します。
ここでは、SDLを例にとります。
SDLを使用することで、ウィンドウを作成し、Lissajous曲線を描画することができます。
完成したプログラム
以下に、SDLを用いたLissajous曲線の描画プログラムの例を示します。
#include <SDL2/SDL.h>
#include <math.h>
#include <stdio.h>
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
#define WIDTH 800
#define HEIGHT 600
int main(int argc, char* argv[]) {
if (SDL_Init(SDL_INIT_VIDEO) != 0) {
printf("SDL_Init Error: %s\n", SDL_GetError());
return 1;
}
SDL_Window* win = SDL_CreateWindow("Lissajous Curve", 100, 100, WIDTH,
HEIGHT, SDL_WINDOW_SHOWN);
if (win == NULL) {
printf("SDL_CreateWindow Error: %s\n", SDL_GetError());
SDL_Quit();
return 1;
}
SDL_Renderer* ren = SDL_CreateRenderer(
win, -1, SDL_RENDERER_ACCELERATED | SDL_RENDERER_PRESENTVSYNC);
if (ren == NULL) {
SDL_DestroyWindow(win);
printf("SDL_CreateRenderer Error: %s\n", SDL_GetError());
SDL_Quit();
return 1;
}
double A = 200, B = 200, a = 3, b = 2, delta = M_PI / 2;
SDL_SetRenderDrawColor(ren, 0, 0, 0, 255);
SDL_RenderClear(ren);
SDL_SetRenderDrawColor(ren, 255, 255, 255, 255);
for (double t = 0; t < 2 * M_PI; t += 0.01) {
int x = (int)(WIDTH / 2 + A * sin(a * t + delta));
int y = (int)(HEIGHT / 2 + B * sin(b * t));
SDL_RenderDrawPoint(ren, x, y);
}
SDL_RenderPresent(ren);
SDL_Delay(5000);
SDL_DestroyRenderer(ren);
SDL_DestroyWindow(win);
SDL_Quit();
return 0;
}このプログラムは、SDLを使用してウィンドウを作成し、Lissajous曲線を描画します。
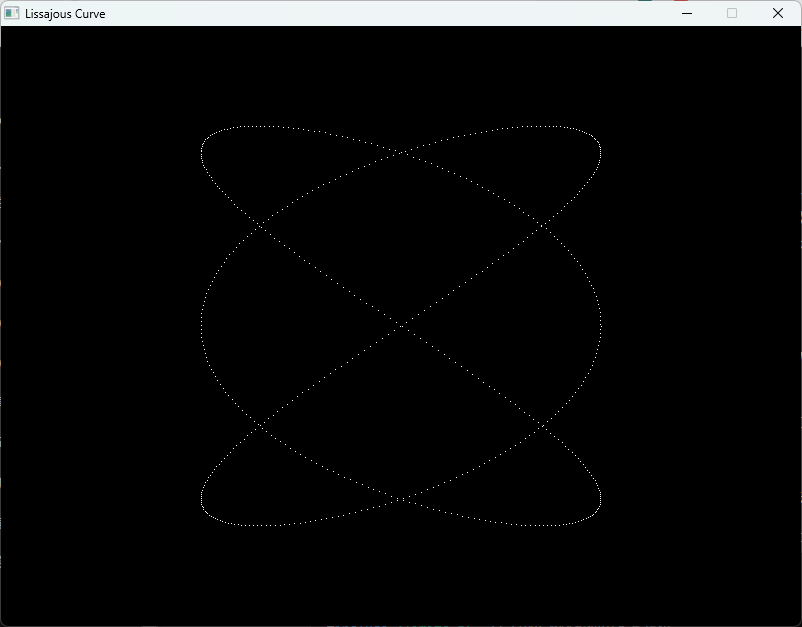
A、B、a、b、deltaの値を変更することで、異なる形状の曲線を描くことができます。
プログラムを実行すると、ウィンドウにLissajous曲線が表示され、5秒後に終了します。
Lissajous曲線の応用
Lissajous曲線は、その美しい形状と数学的特性から、さまざまな分野で応用されています。
以下に、具体的な応用例を紹介します。
オシロスコープでの信号表示
Lissajous曲線は、オシロスコープを用いて2つの異なる周波数の信号を視覚化する際に利用されます。
オシロスコープのX軸とY軸にそれぞれ異なる信号を入力することで、Lissajous曲線が表示されます。
この方法は、信号の周波数比や位相差を直感的に理解するのに役立ちます。
音楽と振動の解析
音楽や振動の解析においても、Lissajous曲線は重要な役割を果たします。
特に、音叉や楽器の振動を視覚化する際に使用され、音の特性を分析するためのツールとして活用されます。
これにより、音楽の調和や不協和音を視覚的に確認することができます。
視覚的パターン生成
Lissajous曲線は、その美しい形状から視覚的なパターン生成にも利用されます。
コンピュータグラフィックスやデジタルアートの分野では、Lissajous曲線を用いて複雑で魅力的なデザインを作成することができます。
これにより、視覚的なインパクトを与える作品を制作することが可能です。
教育用途での利用
教育の現場でも、Lissajous曲線は数学や物理の概念を教えるための効果的なツールとして利用されています。
特に、振動や波動の性質を理解するための教材として、Lissajous曲線を用いた実験やシミュレーションが行われています。
これにより、学生は抽象的な概念を視覚的に理解することができます。
アートとデザインへの応用
Lissajous曲線は、その美しさからアートやデザインの分野でも広く応用されています。
アーティストやデザイナーは、Lissajous曲線を用いて独自の作品を創作し、視覚的な魅力を追求しています。
これにより、Lissajous曲線は単なる数学的な概念を超えて、芸術的な表現の一部としても認識されています。
これらの応用例は、Lissajous曲線が持つ多様な可能性を示しており、科学技術から芸術まで幅広い分野でその価値が認められています。
Lissajous曲線の変形と拡張
Lissajous曲線は、パラメータの調整によってさまざまな形状を描くことができ、その変形と拡張は多くの応用を可能にします。
ここでは、周波数比、位相差、そして3D描画について説明します。
周波数比の影響
Lissajous曲線の形状は、2つの振動の周波数比によって大きく変化します。
周波数比が整数比である場合、曲線は閉じた形状を形成します。
例えば、周波数比が1:1の場合、曲線は直線や円を描きますが、2:1や3:2の場合は、より複雑な形状になります。
| 周波数比 | 形状の例 |
|---|---|
| 1:1 | 円または直線 |
| 2:1 | 8の字型 |
| 3:2 | 花びら型 |
このように、周波数比を変えることで、Lissajous曲線の形状を自在に変化させることができます。
位相差の調整
位相差は、Lissajous曲線の対称性に影響を与えます。
位相差が0またはπの倍数であると、曲線は対称性を持ちますが、位相差を変えることで、曲線の形状が非対称になります。
これにより、より複雑で興味深いパターンを生成することが可能です。
// 例:位相差を調整した座標計算
double delta = M_PI / 4; // 位相差を45度に設定
double x = A * sin(a * t + delta);
double y = B * sin(b * t);3D Lissajous曲線の描画
Lissajous曲線は、3次元空間でも描画することができます。
3D Lissajous曲線は、3つの異なる振動を組み合わせることで生成され、以下のようなパラメトリック方程式で表されます。
- \( x(t) = A \sin(at + \delta_x) \)
- \( y(t) = B \sin(bt + \delta_y) \)
- \( z(t) = C \sin(ct + \delta_z) \)
ここで、\( C \)はz軸方向の振幅、\( c \)はz軸方向の周波数、\( \delta_x \)、\( \delta_y \)、\( \delta_z \)はそれぞれの軸に対する位相差を表します。
3D Lissajous曲線は、より複雑で立体的な形状を描くことができ、視覚的に非常に魅力的です。
3D描画には、OpenGLや他の3Dグラフィックスライブラリを使用することが一般的です。
これにより、Lissajous曲線を3次元空間で視覚化し、回転やズームなどの操作を行うことができます。
これらの技術を駆使することで、Lissajous曲線のさらなる可能性を探求することができます。
まとめ
この記事では、Lissajous曲線の歴史や数学的定義、特徴と性質について詳しく解説し、C言語を用いた描画方法やその応用例についても触れました。
Lissajous曲線は、数学的な美しさと実用性を兼ね備えた曲線であり、科学技術からアートまで幅広い分野で活用されています。
この記事を通じて、Lissajous曲線の多様な可能性に興味を持たれた方は、ぜひ実際にプログラムを作成して、その魅力を体験してみてください。

![[C言語] ドラゴン曲線を計算するプログラムを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44015.png)
![[C言語] トポロジカルソートを実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44014.png)
![[C言語] ハノイの塔を解くプログラムの作成方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44019.png)
![[C言語] はさみうち法(非線形方程式)を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44017.png)
![[C言語] ナップザック問題を動的計画法で解く方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44016.png)
![[C言語] フラクタル圧縮を用いた画像圧縮方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44023.png)
![[C言語] プサイ関数/ポリガンマ関数を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44022.png)
![[C言語] フィボナッチ探索を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44021.png)
![[C言語] フィボナッチ数列を求めるアルゴリズムの書き方](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44020.png)
![[C言語] ベルマンフォード法を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44029.png)
![[C言語] ベータ分布を計算して乱数を生成する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44028.png)
![[C言語] ベータ関数を実装する方法](https://af-e.net/wp-content/uploads/2024/09/thumbnail-44027.png)